
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 829 Атанасян — Подробные Ответы
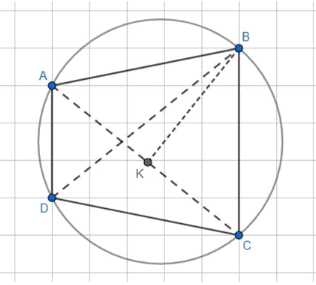
Докажите, что в любом четырёхугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон (теорема Птолемея).
Краткое решение:
1) Возьмем на диагонали AC такую точку K, чтобы углы LABK = 2CBD.
2) Рассмотрим ΔABK и ΔCBD: LBDC = 1/2 LKAB, ΔABK ~ ΔCBD.
3) Рассмотрим ΔBCK и ΔABD: LBKC = 180° — LAKB = 180° — 2C = LA; LBKC = 2DAB, LBCK = LADB = 1/2 U AB.
4) Таким образом, верно равенство: AC = KC + AK = (BC·AD + DC·AB)/BD.
AC·BD = BC·AD + DC·AB.
Полное пошаговое решение:
Дано: Вписанный четырехугольник ABCD, требуется доказать, что \(AC \cdot BD = AD \cdot BC + AB \cdot DC\).
Доказательство:
1) Возьмем на диагонали AC такую точку K, чтобы углы \(LABK = 2CBD\).
2) Рассмотрим треугольники ABK и CBD. Так как \(LBDC = 1/2 LKAB\), то треугольники ABK и CBD подобны (\(ΔABK \sim ΔCBD\)).
3) Из подобия следует, что \(AK/AB = DC/DB\) и \(AK/AC = DC/BC\). Следовательно, \(AK = (AB \cdot DC)/DB\) и \(AK = (AC \cdot DC)/BC\).
4) Рассмотрим треугольники BCK и ABD. Так как \(LBKC = 180° — LAKB = 180° — 2C = LA\), то треугольники BCK и ABD подобны (\(ΔBCK \sim ΔABD\)).
5) Из подобия следует, что \(BC/BD = KC/AD\) и \(BC/AB = KC/DB\). Следовательно, \(KC = (BC \cdot AD)/BD\) и \(KC = (BC \cdot DB)/AB\).
6) Таким образом, \(AC = KC + AK = (BC \cdot AD + DC \cdot AB)/BD\).
7) Умножая обе части на BD, получаем: \(AC \cdot BD = BC \cdot AD + DC \cdot AB\).
Следовательно, доказано, что \(AC \cdot BD = AD \cdot BC + AB \cdot DC\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!