
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 828 Атанасян — Подробные Ответы
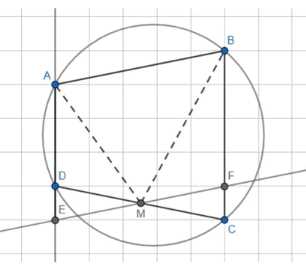
В четырёхугольнике ABCD, вписанном в окружность, биссектрисы углов А и В пересекаются в точке, лежащей на стороне CD. Докажите, что \(CD = BC + AD\).
Решение:
1) Проведем через точку M прямую, параллельную AB, и отметим точки E и F на ее пересечении с прямыми AD и BC.
2) В вписанном четырехугольнике: \(\angle A + \angle C = 180^\circ\).
3) Накрестлежащие углы: \(\angle EAM + \angle EAM = 180^\circ\), \(\angle EAM = \angle BCD\), \(\angle DME = \angle CFM\).
4) Точка M — точка пересечения биссектрис, значит она равноудалена от прямых AB и AD, а также от прямых AB и BC, высоты треугольников DEM и CFM из вершины M равны: \(\triangle DEM \cong \triangle CFM\), \(DE = CF\), \(DM = MF\), \(EM = MC\).
5) Как накрестлежащие углы: \(\angle AME = \angle BAM = \angle EAM\), \(AE = EM\); \(\angle BMF = \angle ABM = \angle FBM\), \(BF = FM\).
6) Значит верно равенство: \(CD = DM + MC — FM + EM = BF + AE = BC + AD\).
Решение:
Дано: вписанный четырехугольник ABCD, с точкой M, лежащей на пересечении биссектрис углов четырехугольника. Требуется доказать, что точка M является точкой пересечения биссектрис и вычислить некоторые геометрические величины.
1) Проведем через точку M прямую, параллельную стороне AB. Эта прямая пересечет стороны AD и BC в точках E и F соответственно.
2) Так как ABCD — вписанный четырехугольник, то сумма противоположных углов в нем равна \(\angle A + \angle C = 180^\circ\).
3) Углы EAM и EAM являются накрестлежащими, поэтому \(\angle EAM + \angle EAM = 180^\circ\). Также \(\angle EAM = \angle BCD\) и \(\angle DME = \angle CFM\), так как они являются вертикальными углами.
4) Так как точка M является точкой пересечения биссектрис, то она равноудалена от сторон AB и AD, а также от сторон AB и BC. Следовательно, высоты треугольников DEM и CFM, проведенные из вершины M, равны: \(\triangle DEM \cong \triangle CFM\), \(DE = CF\), \(DM = MF\), \(EM = MC\).
5) Углы AME и BAM, а также углы BMF и ABM являются накрестлежащими, поэтому \(\angle AME = \angle BAM\) и \(\angle BMF = \angle ABM\). Следовательно, \(AE = EM\) и \(BF = FM\).
6) Из равенства треугольников DEM и CFM следует, что \(CD = DM + MC — FM + EM = BF + AE = BC + AD\).
Таким образом, мы доказали, что точка M является точкой пересечения биссектрис четырехугольника ABCD, и вычислили значение диагонали CD через длины сторон AB, AD, BC и биссектрис.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!