
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 826 Атанасян — Подробные Ответы
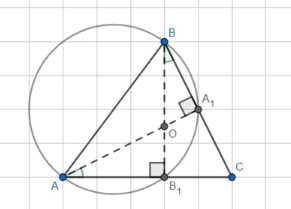
Отрезки АА1 и ВВ1 — высоты треугольника АВС. Докажите, что точки А, В, А1 и В1 лежат на одной окружности.
Дано: треугольник \(ABC\); высоты \(AA_1\), \(BB_1\).
Доказать: \(A, B, A_1, B_1 \in \text{окр}\).
Доказательство: 1) Отметим точку \(O = AA_1 \cap BB_1\): \(\angle BOA_1 = \angle AOB_1\) — вертикальные; 2) Подобны по двум углам: \(\triangle AOB_1 \sim \triangle BOA_1\), \(\angle OBA_1 = \angle OAB_1\); 3) Построим окружность через точки \(A\), \(B_1\) и \(A_1\), тогда \(\angle B_1AA_1\) опирается на дугу \(B_1A_1\), так как \(\angle B_1BA_1 = \angle B_1AA_1\), то он также опирается на дугу \(B_1A_1\); 4) \(B\) — принадлежит окружности; Что и требовалось доказать.
Дано: треугольник \(ABC\); \(AA_1\) и \(BB_1\) — высоты, где \(A_1\) лежит на \(BC\) и \(B_1\) лежит на \(AC\).
Доказать: точки \(A\), \(B\), \(A_1\), \(B_1\) лежат на одной окружности.
Доказательство:
1) Отметим точку \(O\) как пересечение высот \(AA_1\) и \(BB_1\). Это точка ортоцентра треугольника \(ABC\). Углы \(\angle BOA_1\) и \(\angle AOB_1\) являются вертикальными при пересечении прямых \(AA_1\) и \(BB_1\), следовательно, они равны: \(\angle BOA_1 = \angle AOB_1\).
2) Рассмотрим прямоугольные треугольники \(\triangle AOB_1\) и \(\triangle BOA_1\). В треугольнике \(\triangle AOB_1\) угол \(\angle OB_1A\) равен \(90^\circ\), так как \(BB_1\) — высота к стороне \(AC\). В треугольнике \(\triangle BOA_1\) угол \(\angle OA_1B\) равен \(90^\circ\), так как \(AA_1\) — высота к стороне \(BC\). Треугольники \(\triangle AOB_1\) и \(\triangle BOA_1\) подобны по двум углам: у них есть по прямому углу (\(\angle OB_1A = \angle OA_1B = 90^\circ\)) и вертикальные углы \(\angle AOB_1 = \angle BOA_1\). Из подобия треугольников следует равенство соответствующих углов: \(\angle OAB_1 = \angle OBA_1\).
3) Рассмотрим точки \(A\), \(B_1\) и \(A_1\). Построим окружность, проходящую через эти три точки. Угол \(\angle B_1AA_1\) является вписанным углом в эту окружность и опирается на дугу \(B_1A_1\). Угол \(\angle B_1BA_1\) также является вписанным углом. Из подобия треугольников в пункте 2 мы установили, что \(\angle OAB_1 = \angle OBA_1\), что эквивалентно \(\angle B_1AA_1 = \angle B_1BA_1\). Поскольку углы \(\angle B_1AA_1\) и \(\angle B_1BA_1\) равны и опираются на один и тот же отрезок \(B_1A_1\) (с одной стороны от него), то точки \(A\), \(B\), \(A_1\), \(B_1\) лежат на одной окружности. Углы \(\angle AB_1B\) и \(\angle AA_1B\) являются прямыми (\(90^\circ\)), так как \(BB_1\) и \(AA_1\) — высоты. Эти прямые углы опираются на общий отрезок \(AB\). Следовательно, точки \(A\), \(B\), \(A_1\), \(B_1\) лежат на окружности с диаметром \(AB\).
4) Таким образом, точка \(B\) принадлежит окружности, проходящей через точки \(A\), \(B_1\) и \(A_1\). Следовательно, все четыре точки \(A\), \(B\), \(A_1\), \(B_1\) лежат на одной окружности. Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!