
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 825 Атанасян — Подробные Ответы
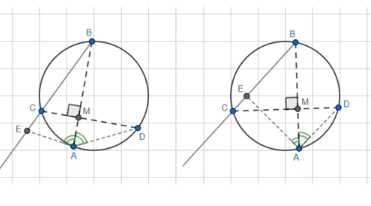
Хорды АВ и CD взаимно перпендикулярны, луч АВ является биссектрисой угла DAE. Докажите, что \(AE \perp BC\). Рассмотрите все возможные случаи.
Дано: \(AB \perp CD\) — хорды; \(AB\) — бисс. \(\angle DAE\). Доказать: \(AE \perp BC\). Доказательство: 1) Отметим точки \(M = AB \cap CD\) и \(E = AE \cap BC\). 2) Опираются на одну дугу: \(\angle EBA = \angle CDA = \frac{1}{2} \cup CA\). 3) В прямоугольном \(\triangle DMA\): \(\angle DAB = 90^\circ — \angle CDA = \angle BAE\). \(\angle DAB = 90^\circ — \angle EBA = \angle BAE\). \(\angle AEB = 180^\circ — \angle EBA — \angle BAE\). \(\angle AEB = 90^\circ\); \(E \in BC\); \(AE \perp BC\). Что и требовалось доказать.
Дано: хорды \(AB \perp CD\); \(AB\) — биссектриса \(\angle DAE\). Доказать: \(AE \perp BC\).
Доказательство:
Отметим точки \(M\) и \(E\). Точка \(M\) является пересечением хорд \(AB\) и \(CD\), то есть \(M = AB \cap CD\). Точка \(E\) является пересечением прямой \(AE\) и хорды \(BC\), то есть \(E = AE \cap BC\).
Углы \(\angle EBA\) и \(\angle CDA\) являются вписанными углами, опирающимися на одну и ту же дугу \(CA\). Следовательно, они равны: \(\angle EBA = \angle CDA\). Мера вписанного угла равна половине меры дуги, на которую он опирается, поэтому \(\angle EBA = \angle CDA = \frac{1}{2} \cup CA\).
Рассмотрим треугольник \(\triangle DMA\). Поскольку хорды \(AB\) и \(CD\) перпендикулярны, угол \(\angle AMD\) является прямым, равным \(90^\circ\). Таким образом, \(\triangle DMA\) является прямоугольным треугольником. В прямоугольном треугольнике сумма острых углов равна \(90^\circ\). Следовательно, \(\angle DAM + \angle CDA = 90^\circ\). Угол \(\angle DAM\) — это тот же угол, что и \(\angle DAB\). Поэтому \(\angle DAB = 90^\circ — \angle CDA\).
По условию, \(AB\) является биссектрисой угла \(\angle DAE\). Это означает, что угол \(\angle DAB\) равен углу \(\angle BAE\): \(\angle DAB = \angle BAE\).
Из равенств \(\angle DAB = 90^\circ — \angle CDA\) и \(\angle DAB = \angle BAE\) следует, что \(90^\circ — \angle CDA = \angle BAE\).
Используя равенство \(\angle CDA = \angle EBA\), полученное ранее, подставим его в последнее уравнение: \(90^\circ — \angle EBA = \angle BAE\). Перегруппируем слагаемые: \(90^\circ = \angle EBA + \angle BAE\).
Теперь рассмотрим треугольник \(\triangle AEB\). Сумма углов в любом треугольнике равна \(180^\circ\). Следовательно, \(\angle AEB + \angle EBA + \angle BAE = 180^\circ\). Подставим значение суммы углов \(\angle EBA + \angle BAE\), которое мы нашли: \(\angle AEB + 90^\circ = 180^\circ\). Вычитая \(90^\circ\) из обеих частей уравнения, получаем \(\angle AEB = 90^\circ\).
Поскольку угол \(\angle AEB\) равен \(90^\circ\) и точка \(E\) лежит на отрезке \(BC\), это означает, что прямая \(AE\) перпендикулярна прямой \(BC\), то есть \(AE \perp BC\). Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!