ГДЗ по Геометрии 11 класс Номер 824 Атанасян — Подробные Ответы

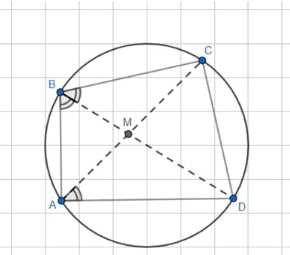
Точки А, В, С и D лежат на одной окружности, луч BD содержит биссектрису ВМ треугольника АВС. Докажите, что \(\angle AMD = \angle BAD\).

Точки A, B, C и D лежат на окружности. BM является биссектрисой угла ABC и лежит на луче BD. Необходимо доказать, что \(\angle AMD = \angle BAD\).

Пусть точка M — пересечение BD и AC. Углы, опирающиеся на одну дугу, равны: \(\angle DBC = \angle DAC\). BM — биссектриса угла ABC.
\(\angle AMD = 180^\circ — \angle DAC — \angle ADB\).
\(\angle BAD = 180^\circ — \angle ABD — \angle ADB\).
Так как \(\angle ABD = \angle DBC\) и \(\angle DBC = \angle DAC\), то \(\angle ABD = \angle DAC\).
Следовательно, \(\angle AMD = 180^\circ — \angle ABD — \angle ADB\).
Таким образом, \(\angle AMD = \angle BAD\). Что и требовалось доказать.

Даны точки A, B, C и D, лежащие на окружности. Известно, что BM является биссектрисой угла ABC, и точка M лежит на луче BD. Требуется доказать, что \(\angle AMD = \angle BAD\).

Пусть точка M является точкой пересечения диагоналей BD и AC четырехугольника ABCD, вписанного в окружность. Углы, опирающиеся на одну и ту же дугу окружности, равны. Так, углы \(\angle DBC\) и \(\angle DAC\) опираются на дугу CD, следовательно, \(\angle DBC = \angle DAC\).

По условию, BM является биссектрисой угла \(\angle ABC\). Поскольку точка M лежит на луче BD, это означает, что прямая BD является биссектрисой угла \(\angle ABC\). Таким образом, угол \(\angle ABD\) равен углу \(\angle DBC\), то есть \(\angle ABD = \angle DBC\).

Из равенств \(\angle DBC = \angle DAC\) и \(\angle ABD = \angle DBC\) следует, что \(\angle ABD = \angle DAC\).

Рассмотрим треугольник AMD. Сумма углов в треугольнике равна 180 градусам. Следовательно, угол \(\angle AMD\) можно выразить как \(180^\circ — \angle MAD — \angle MDA\). Угол \(\angle MAD\) является частью угла \(\angle CAD\), который равен \(\angle DAC\). Угол \(\angle MDA\) является частью угла \(\angle BDA\), который равен \(\angle ADB\). Таким образом, \(\angle AMD = 180^\circ — \angle DAC — \angle ADB\).

Теперь рассмотрим угол \(\angle BAD\). В треугольнике ABD сумма углов равна 180 градусам. Следовательно, угол \(\angle BAD\) можно выразить как \(180^\circ — \angle ABD — \angle ADB\).

Мы ранее установили, что \(\angle ABD = \angle DAC\). Подставим это равенство в выражение для угла \(\angle BAD\): \(\angle BAD = 180^\circ — \angle DAC — \angle ADB\).

Сравнивая выражения для \(\angle AMD\) и \(\angle BAD\), мы видим, что \(\angle AMD = 180^\circ — \angle DAC — \angle ADB\) и \(\angle BAD = 180^\circ — \angle DAC — \angle ADB\). Отсюда следует, что \(\angle AMD = \angle BAD\).

Что и требовалось доказать.