
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 823 Атанасян — Подробные Ответы
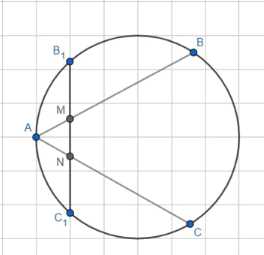
Точки В1 и С1 — середины дуг АВ и АС (рис. 209). Докажите, что \(AM= AN\).
Решение: Угол между двумя пересекающимися хордами равен половине суммы мер дуг, заключенных между ними. Для углов \( \angle AMC_1 \) и \( \angle ANB_1 \) имеем: \( \angle AMC_1 = \frac{1}{2} (\text{дуга } AC_1 + \text{дуга } BB_1) \) и \( \angle ANB_1 = \frac{1}{2} (\text{дуга } AB_1 + \text{дуга } CC_1) \). Поскольку \(B_1\) является серединой дуги \(AB\), то \( \text{дуга } AB_1 = \text{дуга } BB_1 \). Поскольку \(C_1\) является серединой дуги \(AC\), то \( \text{дуга } AC_1 = \text{дуга } CC_1 \). Подставляя эти равенства в формулы для углов, получаем: \( \angle AMC_1 = \frac{1}{2} (\text{дуга } AC_1 + \text{дуга } AB_1) \) и \( \angle ANB_1 = \frac{1}{2} (\text{дуга } AC_1 + \text{дуга } AB_1) \). Следовательно, \( \angle AMC_1 = \angle ANB_1 \). В треугольнике \(AMN\) углы при основании \(MN\) равны (\( \angle AMN = \angle AMC_1 \) и \( \angle ANM = \angle ANB_1 \)), поэтому треугольник \(AMN\) является равнобедренным с основанием \(MN\). Отсюда следует, что боковые стороны равны, то есть \( AM = AN \). Что и требовалось доказать.
Дано: Окружность. Точки \(B_1\) и \(C_1\) являются серединами дуг \(AB\) и \(AC\) соответственно.
Доказать: \(AM = AN\).
Доказательство:
Рассмотрим углы \( \angle AMC_1 \) и \( \angle ANB_1 \). Эти углы являются углами между пересекающимися хордами в окружности. Согласно теореме об угле между двумя пересекающимися хордами, величина такого угла равна половине суммы мер дуг, заключенных между сторонами этого угла и их вертикальным углом.
Для угла \( \angle AMC_1 \), который образован пересечением хорд \(AC\) и \(B_1C_1\), дугами, заключенными между его сторонами, являются дуга \(AC_1\) и дуга \(BB_1\). Поэтому, \( \angle AMC_1 = \frac{1}{2} (\text{мера дуги } AC_1 + \text{мера дуги } BB_1) \).
Для угла \( \angle ANB_1 \), который образован пересечением хорд \(AB\) и \(B_1C_1\), дугами, заключенными между его сторонами, являются дуга \(AB_1\) и дуга \(CC_1\). Поэтому, \( \angle ANB_1 = \frac{1}{2} (\text{мера дуги } AB_1 + \text{мера дуги } CC_1) \).
По условию, точка \(B_1\) является серединой дуги \(AB\). Это означает, что мера дуги \(AB_1\) равна мере дуги \(B_1B\), то есть \( \text{мера дуги } AB_1 = \text{мера дуги } BB_1 \).
Также по условию, точка \(C_1\) является серединой дуги \(AC\). Это означает, что мера дуги \(AC_1\) равна мере дуги \(C_1C\), то есть \( \text{мера дуги } AC_1 = \text{мера дуги } CC_1 \).
Теперь подставим эти равенства в формулы для углов \( \angle AMC_1 \) и \( \angle ANB_1 \).
\( \angle AMC_1 = \frac{1}{2} (\text{мера дуги } AC_1 + \text{мера дуги } BB_1) \)
Заменим \( \text{мера дуги } BB_1 \) на \( \text{мера дуги } AB_1 \):
\( \angle AMC_1 = \frac{1}{2} (\text{мера дуги } AC_1 + \text{мера дуги } AB_1) \).
\( \angle ANB_1 = \frac{1}{2} (\text{мера дуги } AB_1 + \text{мера дуги } CC_1) \)
Заменим \( \text{мера дуги } CC_1 \) на \( \text{мера дуги } AC_1 \):
\( \angle ANB_1 = \frac{1}{2} (\text{мера дуги } AB_1 + \text{мера дуги } AC_1) \).
Сравнивая полученные выражения для \( \angle AMC_1 \) и \( \angle ANB_1 \), видим, что они равны:
\( \angle AMC_1 = \frac{1}{2} (\text{мера дуги } AC_1 + \text{мера дуги } AB_1) \)
\( \angle ANB_1 = \frac{1}{2} (\text{мера дуги } AC_1 + \text{мера дуги } AB_1) \)
Следовательно, \( \angle AMC_1 = \angle ANB_1 \).
Теперь рассмотрим треугольник \(AMN\). Угол \( \angle AMN \) совпадает с углом \( \angle AMC_1 \), а угол \( \angle ANM \) совпадает с углом \( \angle ANB_1 \). Таким образом, в треугольнике \(AMN\) углы при основании \(MN\) равны: \( \angle AMN = \angle ANM \).
Треугольник, у которого углы при основании равны, является равнобедренным. В равнобедренном треугольнике стороны, противолежащие равным углам, равны. В треугольнике \(AMN\) углу \( \angle AMN \) противолежит сторона \(AN\), а углу \( \angle ANM \) противолежит сторона \(AM\). Поскольку \( \angle AMN = \angle ANM \), то \( AN = AM \), или \( AM = AN \).
Таким образом, мы доказали, что \(AM = AN\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!