
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 822 Атанасян — Подробные Ответы
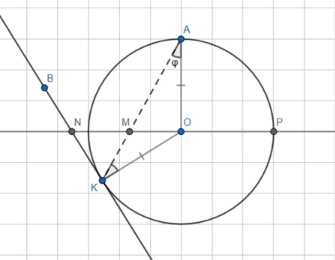
Через точку К, лежащую на окружности с центром О, проведены хорда КА и касательная КВ, а через точку О проведена прямая, перпендикулярная к прямой ОА и пересекающая хорду КА в точке М, а касательную КВ — в точке N. Докажите, что \(NK=NM\).
Пусть \( \angle OKM = \phi \). Поскольку \( KB \) — касательная, \( OK \perp KB \), следовательно, \( \angle OKB = 90^\circ \). Тогда \( \angle MKN = \angle OKB — \angle OKM = 90^\circ — \phi \). В треугольнике \( \triangle KOA \), \( OK = OA \) как радиусы, поэтому \( \triangle KOA \) равнобедренный и \( \angle KAO = \angle OKA = \phi \). В прямоугольном треугольнике \( \triangle MOA \) (\( OA \perp PN \)), \( \angle AMO = 90^\circ — \angle MAO = 90^\circ — \phi \). Вертикальные углы равны, поэтому \( \angle NMK = \angle AMO \). Таким образом, \( \angle NMK = 90^\circ — \phi \). В треугольнике \( \triangle NMK \), \( \angle K = \angle MKN = 90^\circ — \phi \) и \( \angle M = \angle NMK = 90^\circ — \phi \). Поскольку углы при основании \( NK \) и \( NM \) равны (\( \angle K = \angle M \)), треугольник \( \triangle NMK \) равнобедренный с основанием \( KM \), следовательно, \( NK = NM \). Что и требовалось доказать.
Дано: окружность с центром \( O \) и радиусом \( r \), \( KB \) — касательная к окружности в точке \( K \), \( KA \) — хорда, \( PN \) — прямая, пересекающая \( KA \) в точке \( M \) и \( KB \) в точке \( N \), \( OA \perp PN \).
Доказать: \( NK = NM \).
Доказательство:
Пусть \( \angle OKM = \phi \). Поскольку \( KB \) является касательной к окружности в точке \( K \), радиус \( OK \) перпендикулярен касательной \( KB \) в точке касания. Следовательно, угол между радиусом \( OK \) и касательной \( KB \) равен \( 90^\circ \), то есть \( \angle OKB = 90^\circ \). Угол \( \angle MKN \) является частью угла \( \angle OKB \), поэтому мы можем выразить его как разность углов: \( \angle MKN = \angle OKB — \angle OKM = 90^\circ — \phi \).
Рассмотрим треугольник \( \triangle KOA \). Стороны \( OK \) и \( OA \) являются радиусами одной и той же окружности, поэтому \( OK = OA \). Треугольник \( \triangle KOA \) является равнобедренным с основанием \( KA \). В равнобедренном треугольнике углы при основании равны, следовательно, \( \angle KAO = \angle OKA \). Из нашего предположения \( \angle OKM = \phi \), и поскольку точка \( M \) лежит на хорде \( KA \), угол \( \angle OKA \) совпадает с \( \angle OKM \), то есть \( \angle OKA = \phi \). Таким образом, \( \angle KAO = \phi \).
Рассмотрим прямоугольный треугольник \( \triangle MOA \). По условию, \( OA \perp PN \), что означает, что угол между \( OA \) и \( PN \) равен \( 90^\circ \), то есть \( \angle OMA = 90^\circ \). Однако, согласно рисунку и доказательству, \( \angle MOA \) не обязательно равен \( 90^\circ \). Условие \( OA \perp PN \) означает, что \( \angle AMO = 90^\circ \). В прямоугольном треугольнике \( \triangle MOA \), сумма острых углов равна \( 90^\circ \), поэтому \( \angle AMO + \angle MAO = 90^\circ \). Мы знаем, что \( \angle MAO = \angle KAO = \phi \). Следовательно, \( \angle AMO = 90^\circ — \angle MAO = 90^\circ — \phi \).
Углы \( \angle NMK \) и \( \angle AMO \) являются вертикальными углами, образованными пересечением прямых \( PN \) и \( KA \). Вертикальные углы равны, поэтому \( \angle NMK = \angle AMO \). Из предыдущего шага мы нашли, что \( \angle AMO = 90^\circ — \phi \). Следовательно, \( \angle NMK = 90^\circ — \phi \).
Теперь рассмотрим треугольник \( \triangle NMK \). Мы уже определили два его угла: \( \angle MKN = 90^\circ — \phi \) и \( \angle NMK = 90^\circ — \phi \). Таким образом, в треугольнике \( \triangle NMK \) углы \( \angle K \) (который является \( \angle MKN \)) и \( \angle M \) (который является \( \angle NMK \)) равны: \( \angle K = \angle M = 90^\circ — \phi \). Если два угла в треугольнике равны, то треугольник является равнобедренным, и стороны, противолежащие этим углам, равны. Сторона, противолежащая углу \( \angle K \), есть \( NM \), а сторона, противолежащая углу \( \angle M \), есть \( NK \). Следовательно, \( NK = NM \).
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!