ГДЗ по Геометрии 11 класс Номер 821 Атанасян — Подробные Ответы

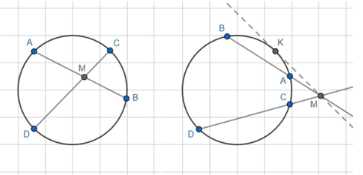
Окружность отсекает на двух прямых, которые пересекаются в точке, не лежащей на окружности, равные хорды. Докажите, что расстояния от точки пересечения этих прямых до концов той и другой хорды соответственно равны между собой.

Дано: окружность; хорды \(AB = CD\); \(AB \cap CD = M\).
Доказать: \(AM = CM\); \(BM = MD\).

Доказательство:
1) Если точка \(M\) лежит внутри круга, тогда по теореме о произведении отрезков пересекающихся хорд имеем \(AM \cdot MB = CM \cdot MD\). Дано, что \(AB = CD\). Также \(MB = AB — AM\) и \(MD = CD — CM\). Подставим это в первое равенство: \(AM \cdot (AB — AM) = CM \cdot (CD — CM)\). Так как \(AB = CD\), то \(AM \cdot (AB — AM) = CM \cdot (AB — CM)\). Раскрывая скобки, получаем \(AM \cdot AB — AM^2 = CM \cdot AB — CM^2\). Перегруппируем члены: \(AM \cdot AB — CM \cdot AB = AM^2 — CM^2\), что равно \(AB(AM — CM) = (AM — CM)(AM + CM)\). Перенесем все в одну сторону: \(AB(AM — CM) — (AM — CM)(AM + CM) = 0\), или \((AM — CM)(AB — (AM + CM)) = 0\). Поскольку \(AB\), \(AM\), \(CM\) — длины отрезков хорд, и в случае пересечения внутри круга \(AB > AM + CM\), то \(AB — (AM + CM) \ne 0\). Следовательно, \(AM — CM = 0\), откуда \(AM = CM\). Поскольку \(AB = CD\) и \(AM = CM\), то \(MB = AB — AM\) и \(MD = CD — CM = AB — AM\), откуда следует \(MB = MD\).

2) Если точка \(M\) лежит вне круга, тогда по теореме о касательной и секущей или двух секущих, проведенных из одной точки вне круга (в данном случае две секущие), имеем \(MA \cdot MB = MC \cdot MD\). Дано, что \(AB = CD\). Также \(MB = MA + AB\) и \(MD = MC + CD\). Подставим это в первое равенство: \(MA \cdot (MA + AB) = MC \cdot (MC + CD)\). Так как \(AB = CD\), то \(MA \cdot (MA + AB) = MC \cdot (MC + AB)\). Раскрывая скобки, получаем \(MA^2 + MA \cdot AB = MC^2 + MC \cdot AB\). Перегруппируем члены: \(MA^2 — MC^2 = MC \cdot AB — MA \cdot AB\), что равно \((MA — MC)(MA + MC) = AB(MC — MA)\). Перенесем все в одну сторону: \((MA — MC)(MA + MC) — AB(MC — MA) = 0\), или \((MA — MC)(MA + MC) + AB(MA — MC) = 0\). Вынесем общий множитель \((MA — MC)\): \((MA — MC)(MA + MC + AB) = 0\). Поскольку \(MA\), \(MC\), \(AB\) — длины отрезков, то \(MA + MC + AB > 0\). Следовательно, \(MA — MC = 0\), откуда \(MA = MC\). Поскольку \(AB = CD\) и \(MA = MC\), то \(MB = MA + AB\) и \(MD = MC + CD = MA + AB\), откуда следует \(MB = MD\).

В обоих случаях доказано, что \(AM = CM\) и \(BM = MD\). Что и требовалось доказать.

Дано: окружность; хорды \(AB\) и \(CD\), причем \(AB = CD\); хорды пересекаются в точке \(M\), то есть \(AB \cap CD = M\).
Доказать: \(AM = CM\) и \(BM = MD\).

Доказательство:

Рассмотрим два случая расположения точки \(M\).

Случай 1: Точка \(M\) лежит внутри круга.
По теореме о произведении отрезков пересекающихся хорд, если две хорды \(AB\) и \(CD\) пересекаются в точке \(M\) внутри круга, то произведение отрезков одной хорды равно произведению отрезков другой хорды. То есть, \(AM \cdot MB = CM \cdot MD\).
Из условия дано, что длины хорд равны: \(AB = CD\).
Так как точка \(M\) лежит между концами хорд, отрезки \(MB\) и \(MD\) могут быть выражены как разность длины всей хорды и соответствующего отрезка:
\(MB = AB — AM\)
\(MD = CD — CM\)
Подставим эти выражения в равенство \(AM \cdot MB = CM \cdot MD\):
\(AM \cdot (AB — AM) = CM \cdot (CD — CM)\)
Поскольку \(AB = CD\), заменим \(CD\) на \(AB\) в правой части уравнения:
\(AM \cdot (AB — AM) = CM \cdot (AB — CM)\)
Раскроем скобки в обеих частях уравнения:
\(AM \cdot AB — AM^2 = CM \cdot AB — CM^2\)
Перенесем все члены в одну сторону, чтобы сгруппировать их:
\(AM \cdot AB — CM \cdot AB — AM^2 + CM^2 = 0\)
Вынесем общий множитель \(AB\) из первых двух членов и используем формулу разности квадратов для последних двух членов:
\(AB(AM — CM) — (AM^2 — CM^2) = 0\)
\(AB(AM — CM) — (AM — CM)(AM + CM) = 0\)
Теперь вынесем общий множитель \((AM — CM)\):
\((AM — CM)(AB — (AM + CM)) = 0\)
\((AM — CM)(AB — AM — CM) = 0\)
Это уравнение имеет два возможных решения: либо \(AM — CM = 0\), либо \(AB — AM — CM = 0\).
Если \(M\) находится внутри круга и является точкой пересечения хорд \(AB\) и \(CD\), то \(AM + MB = AB\) и \(CM + MD = CD\). Сумма отрезков \(AM\) и \(CM\) не равна длине хорды \(AB\) (или \(CD\)), если только \(M\) не совпадает с одним из концов хорд, что противоречит условию пересечения. Более строго, в случае пересечения внутри круга, \(AM < AB\) и \(CM < CD\), и \(AM + CM\) не обязательно равно \(AB\). Однако, если \(AM \ne CM\), то \(AB - AM - CM\) не обязательно равно нулю. Вернемся к уравнению \(AM \cdot AB - AM^2 = CM \cdot AB - CM^2\). Перенесем члены так: \(AM \cdot AB - CM \cdot AB = AM^2 - CM^2\). Вынесем \(AB\): \(AB(AM - CM) = (AM - CM)(AM + CM)\). Перенесем все в левую часть: \(AB(AM - CM) - (AM - CM)(AM + CM) = 0\). Вынесем общий множитель \((AM - CM)\): \((AM - CM)(AB - (AM + CM)) = 0\). Так как \(M\) - точка пересечения внутри круга, \(AM > 0\), \(CM > 0\), \(AB > 0\). Если бы \(AB — AM — CM = 0\), то \(AB = AM + CM\). Это возможно только если \(M\) лежит на отрезке, соединяющем концы хорд, что не является общим случаем пересечения хорд. В общем случае, \(AB — AM — CM \ne 0\).
Следовательно, единственная возможность для равенства быть верным — это \(AM — CM = 0\), откуда следует \(AM = CM\).
Теперь, используя \(AB = CD\) и \(AM = CM\), найдем \(BM\) и \(MD\):
\(BM = AB — AM\)
\(MD = CD — CM\)
Подставим \(AB = CD\) и \(AM = CM\):
\(BM = AB — AM\)
\(MD = AB — AM\)
Таким образом, \(BM = MD\).

Случай 2: Точка \(M\) лежит вне круга.
В этом случае \(M\) является точкой пересечения прямых, содержащих хорды \(AB\) и \(CD\). Пусть прямые \(AB\) и \(CD\) пересекаются в точке \(M\) вне круга. По теореме о двух секущих, проведенных из одной точки вне круга, произведение внешней части одной секущей на всю секущую равно произведению внешней части другой секущей на всю другую секущую. То есть, \(MA \cdot MB = MC \cdot MD\).
Из условия дано, что длины хорд равны: \(AB = CD\).
Так как точка \(M\) лежит вне круга, отрезки \(MB\) и \(MD\) могут быть выражены как сумма расстояния от \(M\) до ближайшей точки пересечения с окружностью и длины хорды:
\(MB = MA + AB\)
\(MD = MC + CD\)
Подставим эти выражения в равенство \(MA \cdot MB = MC \cdot MD\):
\(MA \cdot (MA + AB) = MC \cdot (MC + CD)\)
Поскольку \(AB = CD\), заменим \(CD\) на \(AB\) в правой части уравнения:
\(MA \cdot (MA + AB) = MC \cdot (MC + AB)\)
Раскроем скобки в обеих частях уравнения:
\(MA^2 + MA \cdot AB = MC^2 + MC \cdot AB\)
Перенесем все члены в одну сторону:
\(MA^2 — MC^2 + MA \cdot AB — MC \cdot AB = 0\)
Используем формулу разности квадратов для первых двух членов и вынесем общий множитель \(AB\) из последних двух членов:
\((MA — MC)(MA + MC) + AB(MA — MC) = 0\)
Теперь вынесем общий множитель \((MA — MC)\):
\((MA — MC)(MA + MC + AB) = 0\)
Это уравнение имеет два возможных решения: либо \(MA — MC = 0\), либо \(MA + MC + AB = 0\).
Поскольку \(M\) находится вне круга, \(MA\), \(MC\), \(AB\) — положительные длины отрезков. Сумма положительных чисел \(MA + MC + AB\) всегда больше нуля, то есть \(MA + MC + AB \ne 0\).
Следовательно, единственная возможность для равенства быть верным — это \(MA — MC = 0\), откуда следует \(MA = MC\).
Теперь, используя \(AB = CD\) и \(MA = MC\), найдем \(MB\) и \(MD\):
\(MB = MA + AB\)
\(MD = MC + CD\)
Подставим \(AB = CD\) и \(MA = MC\):
\(MB = MA + AB\)
\(MD = MA + AB\)
Таким образом, \(MB = MD\).

В обоих случаях, когда точка \(M\) лежит внутри круга и когда она лежит вне круга, мы доказали, что \(AM = CM\) и \(BM = MD\).

Что и требовалось доказать.