
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 819 Атанасян — Подробные Ответы
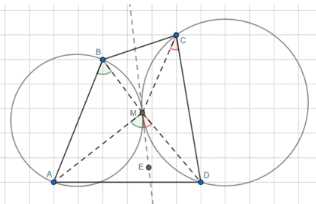
Точка М лежит внутри четырёхугольника ABCD. Докажите, что \(\angle AMD = \angle ABM + \angle MCD\) тогда и только тогда, когда окружности, описанные около треугольников ABM и MCD, имеют в точке М общую касательную.
Через точку \(M\) проведем прямую \(ME\). Если \(ME\) является касательной к окружности, описанной около \(\triangle ABM\), то по теореме об угле между касательной и хордой имеем \(\angle AME = \angle ABM\). Если эта же прямая \(ME\) является касательной к окружности, описанной около \(\triangle MCD\), то аналогично \(\angle DME = \angle MCD\). Тогда \(\angle AMD = \angle AME + \angle DME = \angle ABM + \angle MCD\). Обратно, если \(\angle AMD = \angle ABM + \angle MCD\), и \(\angle AME = \angle ABM\), то \(\angle DME = \angle AMD — \angle AME = (\angle ABM + \angle MCD) — \angle ABM = \angle MCD\). Поскольку \(\angle AME = \angle ABM\) и \(\angle DME = \angle MCD\), прямая \(ME\) по теореме, обратной теореме об угле между касательной и хордой, является касательной к обеим окружностям в точке \(M\).
Дано: четырехугольник \(ABCD\), точка \(M\) лежит внутри \(ABCD\).
Доказать: \(\angle AMD = \angle ABM + \angle MCD\) тогда и только тогда, когда окружности, описанные около \(\triangle ABM\) и \(\triangle MCD\), имеют в точке \(M\) общую касательную.
Доказательство:
Прямое утверждение: Предположим, что окружности, описанные около \(\triangle ABM\) и \(\triangle MCD\), имеют в точке \(M\) общую касательную. Обозначим эту касательную прямую \(ME\), где точка \(E\) лежит на этой прямой.
По теореме об угле между касательной и хордой, угол между касательной \(ME\) и хордой \(AM\) окружности, описанной около \(\triangle ABM\), равен углу, опирающемуся на эту хорду в окружности. Таким образом, \(\angle AME = \angle ABM\).
Аналогично, для окружности, описанной около \(\triangle MCD\), угол между касательной \(ME\) и хордой \(MD\) равен углу, опирающемуся на эту хорду. Следовательно, \(\angle DME = \angle MCD\).
Угол \(\angle AMD\) является суммой углов \(\angle AME\) и \(\angle DME\). То есть, \(\angle AMD = \angle AME + \angle DME\). Подставляя полученные равенства, имеем \(\angle AMD = \angle ABM + \angle MCD\). Таким образом, прямое утверждение доказано.
Обратное утверждение: Предположим, что \(\angle AMD = \angle ABM + \angle MCD\). Проведем через точку \(M\) прямую \(ME\) такую, что \(\angle AME = \angle ABM\).
По теореме, обратной теореме об угле между касательной и хордой, если угол между прямой \(ME\) и хордой \(AM\) равен углу \(\angle ABM\), который опирается на эту хорду в окружности, описанной около \(\triangle ABM\), то прямая \(ME\) является касательной к этой окружности в точке \(M\).
Теперь рассмотрим угол \(\angle DME\). Из условия \(\angle AMD = \angle ABM + \angle MCD\) и построения \(\angle AME = \angle ABM\), следует, что \(\angle DME = \angle AMD — \angle AME\). Подставляя значения, получаем \(\angle DME = (\angle ABM + \angle MCD) — \angle ABM = \angle MCD\).
Таким образом, угол между прямой \(ME\) и хордой \(MD\) равен \(\angle MCD\). Угол \(\angle MCD\) является углом, опирающимся на хорду \(MD\) в окружности, описанной около \(\triangle MCD\). По теореме, обратной теореме об угле между касательной и хордой, если угол между прямой \(ME\) и хордой \(MD\) равен углу \(\angle MCD\), опирающемуся на эту хорду, то прямая \(ME\) является касательной к окружности, описанной около \(\triangle MCD\), в точке \(M\).
Поскольку прямая \(ME\) является касательной как к окружности, описанной около \(\triangle ABM\), так и к окружности, описанной около \(\triangle MCD\), в точке \(M\), то \(ME\) является общей касательной к этим двум окружностям в точке \(M\). Таким образом, обратное утверждение также доказано.
Следовательно, \(\angle AMD = \angle ABM + \angle MCD\) тогда и только тогда, когда окружности, описанные около \(\triangle ABM\) и \(\triangle MCD\), имеют в точке \(M\) общую касательную.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!