Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 818 Атанасян — Подробные Ответы
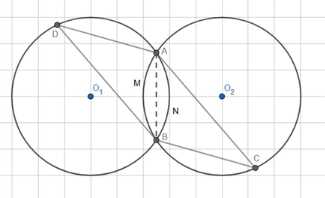
Прямая АС — касательная к окружности с центром O1, а прямая BD — касательная к окружности с центром O2 (рис. 208). Докажите, что: а) AD \| BC; б) \(AB^2= AD \cdot BC\); в) \(\frac{BD^2}{AC^2}= \frac{AD}{BC}\)
По касательной и хорде имеем \(\angle DBA = \frac{1}{2} \cup AMB = \angle BCA\) и \(\angle CAB = \frac{1}{2} \cup ANB = \angle ADB\). По сумме углов треугольника \(\angle DAB = 180^\circ — \angle ADB — \angle DBA = 180^\circ — \angle CAB — \angle BCA\). Так как \(\angle ABC = 180^\circ — \angle CAB — \angle BCA\), то \(\angle DAB = \angle ABC\). Поскольку \(\angle DAB\) и \(\angle ABC\) являются накрестлежащими углами при прямых \(AD\) и \(BC\) и секущей \(AB\), то \(AD \parallel BC\). Треугольники \(\triangle BAD\) и \(\triangle CBA\) подобны по трем углам, так как \(\angle DAB = \angle ABC\), \(\angle ADB = \angle CAB\) и \(\angle DBA = \angle BCA\). Из подобия следует соотношение сторон \(\frac{AB}{CB} = \frac{AD}{AB} = \frac{BD}{CA}\). Из \(\frac{AB}{CB} = \frac{AD}{AB}\) получаем \(AB^2 = AD \cdot CB\). Из \(\frac{AB}{CB} = \frac{BD}{CA}\) получаем \(\frac{BD}{CA} = \frac{AB}{CB}\). Возводя в квадрат обе части, имеем \(\frac{BD^2}{CA^2} = \frac{AB^2}{CB^2}\). Подставляя \(AB^2 = AD \cdot CB\), получаем \(\frac{BD^2}{AC^2} = \frac{AD \cdot CB}{CB^2} = \frac{AD}{CB}\). Таким образом, \(\frac{BD^2}{AC^2} = AD : BC\).
Дано две окружности Окр \(O_1\) с радиусом \(r_1\) и Окр \(O_2\) с радиусом \(r_2\), которые имеют две общие точки \(A\) и \(B\). Прямая \(BD\) является касательной к Окр \(O_2\) в точке \(B\), а прямая \(AC\) является касательной к Окр \(O_1\) в точке \(A\).
Первый шаг доказательства основан на теореме об угле между касательной и хордой. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой меры дуги, заключенной между ними. Для Окр \(O_2\), касательной \(BD\) и хорды \(AB\), угол \(\angle DBA\) равен половине угловой меры дуги \(AMB\), где \(M\) — точка на дуге Окр \(O_2\). Угол \(\angle BCA\) является вписанным углом в Окр \(O_2\), опирающимся на дугу \(AMB\). Следовательно, \(\angle DBA = \frac{1}{2} \cup AMB = \angle BCA\). Аналогично, для Окр \(O_1\), касательной \(AC\) и хорды \(AB\), угол \(\angle CAB\) равен половине угловой меры дуги \(ANB\), где \(N\) — точка на дуге Окр \(O_1\). Угол \(\angle ADB\) является вписанным углом в Окр \(O_1\), опирающимся на дугу \(ANB\). Следовательно, \(\angle CAB = \frac{1}{2} \cup ANB = \angle ADB\).
Второй шаг использует свойство суммы углов треугольника. В треугольнике \(ABD\) сумма углов равна \(180^\circ\), то есть \(\angle DAB + \angle ADB + \angle DBA = 180^\circ\). Отсюда \(\angle DAB = 180^\circ — \angle ADB — \angle DBA\). Используя результаты первого шага, подставим \(\angle ADB = \angle CAB\) и \(\angle DBA = \angle BCA\). Получим \(\angle DAB = 180^\circ — \angle CAB — \angle BCA\). Рассмотрим треугольник \(ABC\). Сумма его углов также равна \(180^\circ\), то есть \(\angle ABC + \angle BCA + \angle CAB = 180^\circ\). Отсюда \(\angle ABC = 180^\circ — \angle CAB — \angle BCA\). Сравнивая выражения для \(\angle DAB\) и \(\angle ABC\), видим, что \(\angle DAB = \angle ABC\). Углы \(\angle DAB\) и \(\angle ABC\) являются накрестлежащими углами при прямых \(AD\) и \(BC\) и секущей \(AB\). Поскольку накрестлежащие углы равны (\(\angle DAB = \angle ABC\)), то прямые \(AD\) и \(BC\) параллельны. Таким образом, доказано, что \(AD \parallel BC\).
Третий шаг основан на подобии треугольников. Рассмотрим треугольники \(\triangle BAD\) и \(\triangle CBA\). У нас уже доказано, что \(\angle DAB = \angle ABC\) и \(\angle ADB = \angle CAB\). Также мы знаем, что \(\angle DBA = \angle BCA\). Поскольку все три угла одного треугольника равны соответствующим углам другого треугольника, то треугольники \(\triangle BAD\) и \(\triangle CBA\) подобны по трем углам. Из подобия треугольников следует пропорциональность их соответствующих сторон. Соответственные стороны лежат напротив равных углов. Напротив \(\angle ADB\) в \(\triangle BAD\) лежит сторона \(AB\), а напротив \(\angle CAB\) в \(\triangle CBA\) лежит сторона \(CB\). Значит, \(\frac{AB}{CB}\). Напротив \(\angle DBA\) в \(\triangle BAD\) лежит сторона \(AD\), а напротив \(\angle BCA\) в \(\triangle CBA\) лежит сторона \(AB\). Значит, \(\frac{AD}{AB}\). Напротив \(\angle BAD\) в \(\triangle BAD\) лежит сторона \(BD\), а напротив \(\angle CBA\) в \(\triangle CBA\) лежит сторона \(CA\). Значит, \(\frac{BD}{CA}\). Таким образом, получаем соотношение \(\frac{AB}{CB} = \frac{AD}{AB} = \frac{BD}{CA}\).
Из первой части этого соотношения \(\frac{AB}{CB} = \frac{AD}{AB}\) путем перемножения крайних и средних членов получаем \(AB \cdot AB = AD \cdot CB\), что равносильно \(AB^2 = AD \cdot BC\). Таким образом, доказано, что \(AB^2 = AD \cdot BC\).
Теперь рассмотрим вторую и третью части соотношения \(\frac{AD}{AB} = \frac{BD}{CA}\). Также можно использовать \(\frac{AB}{CB} = \frac{BD}{CA}\). Из \(\frac{AB}{CB} = \frac{BD}{CA}\) выразим отношение \(\frac{BD}{CA}\). Возведем обе части в квадрат: \(\left(\frac{BD}{CA}\right)^2 = \left(\frac{AB}{CB}\right)^2\), что дает \(\frac{BD^2}{CA^2} = \frac{AB^2}{CB^2}\). Мы уже доказали, что \(AB^2 = AD \cdot BC\). Подставим это выражение для \(AB^2\) в правую часть равенства: \(\frac{BD^2}{AC^2} = \frac{AD \cdot BC}{BC^2}\). Сокращая \(BC\) в числителе и знаменателе, получаем \(\frac{BD^2}{AC^2} = \frac{AD}{BC}\). Это можно записать как \(\frac{BD^2}{AC^2} = AD : BC\). Таким образом, доказано, что \(\frac{BD^2}{AC^2} = AD : BC\).
Все три части утверждения доказаны.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.