
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 817 Атанасян — Подробные Ответы
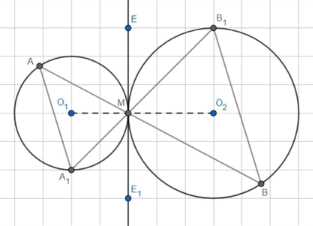
Две окружности имеют единственную общую точку М. Через эту точку проведены две секущие, пересекающие одну окружность в точках А и А1, а другую — в точках В и В1. Докажите, что АА1 \| ВВ1.
Построим общую касательную ME, тогда \(O_1M \perp ME\) и \(O_2M \perp ME\). Отметим на прямой ME точку \(E_1\). Между касательной и хордой имеем: \(\angle EMB_1 = \frac{1}{2} \cup MB_1 = \angle MBB_1\) и \(\angle A_1ME_1 = \frac{1}{2} \cup A_1M = \angle A_1AM\). Вертикальные углы равны: \(\angle EMB_1 = \angle A_1ME_1\). Следовательно, \(\angle A_1AM = \angle MBB_1\). Так как эти углы являются накрестлежащими при прямых \(AA_1\) и \(BB_1\) и секущей \(AB\), то \(AA_1 \parallel BB_1\), что и требовалось доказать.
Дано две окружности с центрами \(O_1\) и \(O_2\) и радиусами \(r_1\) и \(r_2\) соответственно, имеющие общую точку \(M\). Прямые \(A_1B_1\) и \(AB\) являются секущими, проходящими через точку \(M\), причем точки \(A, A_1\) лежат на первой окружности, а точки \(B, B_1\) лежат на второй окружности. Требуется доказать, что прямые \(AA_1\) и \(BB_1\) параллельны.
Для доказательства построим общую касательную к обеим окружностям, проходящую через точку \(M\). Обозначим эту касательную как прямую \(ME\). По свойству касательной, проведенной к окружности через точку касания, радиус, проведенный в эту точку, перпендикулярен касательной. Следовательно, \(O_1M \perp ME\) и \(O_2M \perp ME\). Отметим на прямой \(ME\) точку \(E_1\) так, чтобы точки \(E, M, E_1\) лежали на одной прямой.
Рассмотрим первую окружность с центром \(O_1\). Угол между касательной \(ME\) и хордой \(A_1M\) равен половине угловой величины дуги \(A_1M\), заключенной между ними. То есть, \(\angle A_1ME_1 = \frac{1}{2} \cup A_1M\). Вписанный угол \(A_1AM\) опирается на ту же дугу \(A_1M\), следовательно, его величина также равна половине угловой величины этой дуги: \(\angle A_1AM = \frac{1}{2} \cup A_1M\). Отсюда следует, что \(\angle A_1ME_1 = \angle A_1AM\).
Аналогично, рассмотрим вторую окружность с центром \(O_2\). Угол между касательной \(ME\) и хордой \(MB_1\) равен половине угловой величины дуги \(MB_1\), заключенной между ними. То есть, \(\angle EMB_1 = \frac{1}{2} \cup MB_1\). Вписанный угол \(MBB_1\) опирается на ту же дугу \(MB_1\), следовательно, его величина также равна половине угловой величины этой дуги: \(\angle MBB_1 = \frac{1}{2} \cup MB_1\). Отсюда следует, что \(\angle EMB_1 = \angle MBB_1\).
Углы \(\angle EMB_1\) и \(\angle A_1ME_1\) являются вертикальными углами при пересечении прямых \(ME\) и \(A_1B_1\). Вертикальные углы равны, следовательно, \(\angle EMB_1 = \angle A_1ME_1\).
Из полученных равенств \(\angle A_1ME_1 = \angle A_1AM\) и \(\angle EMB_1 = \angle MBB_1\), а также из равенства вертикальных углов \(\angle EMB_1 = \angle A_1ME_1\), следует, что \(\angle A_1AM = \angle MBB_1\).
Углы \(\angle A_1AM\) и \(\angle MBB_1\) являются накрестлежащими углами при пересечении прямых \(AA_1\) и \(BB_1\) секущей \(AB\). Поскольку накрестлежащие углы равны, это означает, что прямые \(AA_1\) и \(BB_1\) параллельны.
Таким образом, мы доказали, что \(AA_1 \parallel BB_1\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!