Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 816 Атанасян — Подробные Ответы
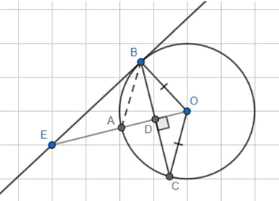
Через точку D, лежащую на радиусе ОА окружности с центром О, проведена хорда ВС, перпендикулярная к ОА, а через точку В проведена касательная к окружности, пересекающая прямую ОА в точке Е. Докажите, что луч ВА — биссектриса угла СВЕ.
Угол между ВЕ и хордой ВА: \(\angle ABE = \frac{1}{2}\) дуги BA; \(\angle ABE = \frac{1}{2}\angle AOB\). В равнобедренном \(\triangle BOC\): OB = OC, OD \(\perp\) BC, \(\angle DOC = \angle DOB\). Угол между хордой ВС и лучом ВА: \(\angle ABC = \frac{1}{2}\) дуги AC = \(\frac{1}{2}\angle AOC = \frac{1}{2}\angle BOA\). \(\angle ABE = \angle ABC = \frac{1}{2}\angle AOB\). Что и требовалось доказать.
Угол между касательной ВЕ и хордой ВА, проведенной из точки касания В, равен половине угловой величины дуги, заключенной между ними, то есть дуги ВА. Угловая величина дуги ВА равна центральному углу, опирающемуся на эту дугу, то есть \(\angle BOA\). Следовательно, \(\angle ABE = \frac{1}{2}\) дуги ВА = \(\frac{1}{2}\angle BOA\).
Рассмотрим треугольник ВОС. Отрезки ОВ и ОС являются радиусами окружности с центром в точке О, поэтому ОВ = ОС. Следовательно, треугольник ВОС является равнобедренным с основанием ВС. По условию, ВС перпендикулярно ОА, и точка D является точкой пересечения ВС и ОА. Таким образом, отрезок OD является высотой в равнобедренном треугольнике ВОС, проведенной к основанию ВС. В равнобедренном треугольнике высота, проведенная к основанию, также является медианой и биссектрисой угла при вершине. Следовательно, OD делит угол ВОС пополам, то есть \(\angle BOD = \angle COD\).
Поскольку отрезок ОА перпендикулярен хорде ВС и проходит через центр окружности О, прямая, содержащая ОА, является осью симметрии для хорды ВС и соответствующей дуги ВС. Следовательно, дуга АВ равна дуге АС.
Поскольку дуга АВ равна дуге АС, центральные углы, опирающиеся на эти дуги, также равны. Центральным углом, опирающимся на дугу АВ, является \(\angle АОВ\), а центральным углом, опирающимся на дугу АС, является \(\angle АОС\). Следовательно, \(\angle АОВ = \angle АОС\).
Угол АВС является вписанным углом, опирающимся на дугу АС. Величина вписанного угла равна половине угловой величины дуги, на которую он опирается. Следовательно, \(\angle ABC = \frac{1}{2}\) дуги АС.
Поскольку дуга АС равна центральному углу \(\angle АОС\), мы имеем \(\angle ABC = \frac{1}{2}\angle АОС\). Используя тот факт, что \(\angle АОС = \angle АОВ\), мы можем записать \(\angle ABC = \frac{1}{2}\angle АОВ\).
Мы получили два выражения: \(\angle ABE = \frac{1}{2}\angle АОВ\) и \(\angle ABC = \frac{1}{2}\angle АОВ\). Из этих равенств следует, что \(\angle ABE = \angle ABC\).
Углы \(\angle ABE\) и \(\angle ABC\) равны, и луч ВА находится между лучами ВЕ и ВС. Следовательно, луч ВА является биссектрисой угла СВЕ. Что и требовалось доказать.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.