ГДЗ по Геометрии 11 класс Номер 815 Атанасян — Подробные Ответы

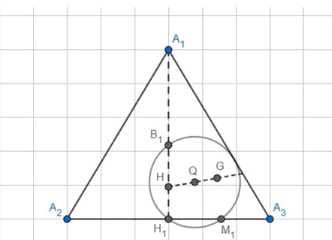
Дан тетраэдр, все высоты которого пересекаются в одной точке. Докажите, что точки пересечения медиан всех граней, основания высот тетраэдра и точки, которые делят каждый из отрезков, соединяющих точку пересечения высот с вершинами, в отношении 2:1, считая от вершины, лежат на одной сфере, центр которой расположен на прямой Эйлера (сфера Эйлера).

Доказательство основано на векторных соотношениях. Сначала показывается, что если \(\vec{HQ} = \frac{2}{3}\vec{HG}\), то точка Q является центром сферы Эйлера. Используются известные соотношения для векторов, такие как \(\vec{A_1B_1} = 2\vec{B_1H}\) и \(\vec{HB_1} = \frac{1}{3}\vec{HA_1}\). Точка \(M_1\) является центроидом грани \(A_2A_3A_4\), и ее радиус-вектор относительно H задается формулой \(\vec{HM_1} = \frac{1}{3}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4})\). Вектор \(\vec{HG}\) определяется как \(\vec{HG} = \frac{1}{4}(\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})\). Вычисляя векторы \(\vec{QM_1} = \vec{HM_1} — \vec{HQ}\) и \(\vec{QB_1} = \vec{HB_1} — \vec{HQ}\) с использованием соотношения \(\vec{HQ} = \frac{2}{3}\vec{HG}\), получаем \(\vec{QM_1} = \frac{1}{6}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4} — \vec{HA_1})\) и \(\vec{QB_1} = -\frac{1}{6}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4} — \vec{HA_1})\). Из этого следует, что \(\vec{QM_1} = -\vec{QB_1}\), что означает, что \(M_1\) и \(B_1\) являются концами диаметра сферы с центром в точке Q. Аналогично показывается, что все точки \(M_i\) и \(B_i\) лежат на этой сфере. Также указывается, что точки \(H_i\) принадлежат этой же сфере.

Доказательство начинается с рассмотрения условия, что если точка Q удовлетворяет векторному равенству \(\vec{HQ} = \frac{2}{3}\vec{HG}\), то она является центром так называемой сферы Эйлера для данного тетраэдра.

Далее используются известные векторные соотношения, связанные с высотами и медианами тетраэдра. В частности, для точки \(B_1\) на высоте \(A_1H_1\) имеем \(\vec{A_1B_1} = 2\vec{B_1H}\), \(\vec{A_1H} = 3\vec{B_1H}\) и \(\vec{HB_1} = \frac{1}{3}\vec{HA_1}\). Эти соотношения описывают положение точки \(B_1\) на отрезке \(A_1H\), делящей его в отношении 2:1, начиная от \(A_1\).

Точка \(M_1\) определена как центроид грани \(A_2A_3A_4\). Радиус-вектор центроида грани относительно произвольной точки H выражается как среднее арифметическое радиус-векторов вершин грани относительно той же точки. Таким образом, \(\vec{HM_1} = \frac{1}{3}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4})\).

Точка G является центроидом всего тетраэдра \(A_1A_2A_3A_4\). Ее радиус-вектор относительно H выражается как среднее арифметическое радиус-векторов всех вершин относительно H: \(\vec{HG} = \frac{1}{4}(\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})\).

Теперь рассмотрим вектор \(\vec{QM_1}\). Его можно найти как разность векторов \(\vec{HM_1}\) и \(\vec{HQ}\): \(\vec{QM_1} = \vec{HM_1} — \vec{HQ}\). Подставляя выражения для \(\vec{HM_1}\) и \(\vec{HQ} = \frac{2}{3}\vec{HG}\), получаем:
\(\vec{QM_1} = \frac{1}{3}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4}) — \frac{2}{3} \cdot \frac{1}{4}(\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})\)
\(\vec{QM_1} = \frac{1}{3}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4}) — \frac{1}{6}(\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})\)
\(\vec{QM_1} = \frac{2(\vec{HA_2} + \vec{HA_3} + \vec{HA_4}) — (\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})}{6}\)
\(\vec{QM_1} = \frac{2\vec{HA_2} + 2\vec{HA_3} + 2\vec{HA_4} — \vec{HA_1} — \vec{HA_2} — \vec{HA_3} — \vec{HA_4}}{6}\)
\(\vec{QM_1} = \frac{1}{6}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4} — \vec{HA_1})\).

Аналогично рассмотрим вектор \(\vec{QB_1}\). Его можно найти как разность векторов \(\vec{HB_1}\) и \(\vec{HQ}\): \(\vec{QB_1} = \vec{HB_1} — \vec{HQ}\). Подставляя выражения для \(\vec{HB_1}\) и \(\vec{HQ}\), получаем:
\(\vec{QB_1} = \frac{1}{3}\vec{HA_1} — \frac{2}{3} \cdot \frac{1}{4}(\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})\)
\(\vec{QB_1} = \frac{1}{3}\vec{HA_1} — \frac{1}{6}(\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})\)
\(\vec{QB_1} = \frac{2\vec{HA_1} — (\vec{HA_1} + \vec{HA_2} + \vec{HA_3} + \vec{HA_4})}{6}\)
\(\vec{QB_1} = \frac{2\vec{HA_1} — \vec{HA_1} — \vec{HA_2} — \vec{HA_3} — \vec{HA_4}}{6}\)
\(\vec{QB_1} = \frac{1}{6}(\vec{HA_1} — \vec{HA_2} — \vec{HA_3} — \vec{HA_4})\)
\(\vec{QB_1} = -\frac{1}{6}(\vec{HA_2} + \vec{HA_3} + \vec{HA_4} — \vec{HA_1})\).

Сравнивая полученные выражения для \(\vec{QM_1}\) и \(\vec{QB_1}\), видим, что \(\vec{QM_1} = -\vec{QB_1}\). Это векторное равенство означает, что точка Q является серединой отрезка \(M_1B_1\).

Согласно задаче 814, квадраты длин векторов \(\vec{QM_i}\) и \(\vec{QB_i}\) равны между собой для всех i, то есть \(QM_1^2 = QM_2^2 = QM_3^2 = QM_4^2 = QB_1^2 = QB_2^2 = QB_3^2 = QB_4^2\). Это означает, что все точки \(M_i\) (центроиды граней) и \(B_i\) (точки, делящие отрезки \(HA_i\) в отношении 2:1) находятся на одинаковом расстоянии от точки Q. Следовательно, все эти точки принадлежат сфере с центром в точке Q.

Наконец, рассматриваются точки \(H_i\), которые являются основаниями высот. Известно, что \(B_1\) и \(H\) лежат на прямой \(A_1H_1\). Точки \(H_1\) и \(M_1\) лежат в плоскости грани \(A_2A_3A_4\), которая перпендикулярна высоте \(A_1H_1\). Утверждается, что точки \(B_1, H_1, M_1\) и \(H_1\) принадлежат сфере Эйлера. Поскольку уже показано, что \(B_1\) и \(M_1\) лежат на сфере с центром Q, это утверждение подразумевает, что \(H_1\) также лежит на этой сфере. Аналогичные рассуждения применимы для точек \(H_2, H_3\) и \(H_4\).

Таким образом, все указанные точки: центроиды всех граней, основания высот и точки, делящие отрезки \(HA_i\) в отношении 2:1, лежат на одной сфере, центром которой является точка Q, расположенная на прямой Эйлера.