ГДЗ по Геометрии 11 класс Номер 813 Атанасян — Подробные Ответы

Шар образован вращением полукруга вокруг прямой, содержащей диаметр. При этом поверхность, образованная вращением некоторой хорды, один конец которой совпадает с концом данного диаметра, разбивает шар на две равные по объёму части. Найдите косинус угла между этой хордой и диаметром.

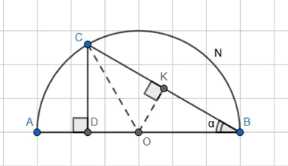
Отметим точку О на середине отрезка АВ, являющуюся центром полукруга и шара. Пусть \(\angle CBA = \alpha\). Поверхность, образованная вращением хорды ВС вокруг диаметра АВ, делит объем шара пополам. Объем части шара, ограниченной этой поверхностью и частью сферы, соответствует объему шарового сегмента, образованного вращением области, ограниченной дугой ВС и отрезком ВС, вокруг АВ. Высота этого шарового сегмента равна проекции ВС на АВ, то есть BD. В прямоугольном треугольнике BCD имеем \(BD = BC \cos \alpha\). В равнобедренном треугольнике OBC (OB = OC = R) высота ОК к ВС делит ВС пополам, и в прямоугольном треугольнике OBK имеем \(BK = OB \cos \alpha = R \cos \alpha\), следовательно \(BC = 2R \cos \alpha\). Тогда \(BD = (2R \cos \alpha) \cos \alpha = 2R \cos^2 \alpha\). Объем шарового сегмента высотой \(h\) равен \(V_{\text{сегмента}} = \frac{1}{3}\pi h^2 (3R — h)\). Подставляя \(h = BD = 2R \cos^2 \alpha\), получаем \(V_{\text{сегмента}} = \frac{1}{3}\pi (2R \cos^2 \alpha)^2 (3R — 2R \cos^2 \alpha) =\)
\(=\frac{1}{3}\pi (4R^2 \cos^4 \alpha) R (3 — 2 \cos^2 \alpha) = \frac{4}{3}\pi R^3 \cos^4 \alpha (3 — 2 \cos^2 \alpha)\). По условию, этот объем равен половине объема шара, который равен \(V_{\text{шара}} = \frac{4}{3}\pi R^3\). Следовательно, \(\frac{4}{3}\pi R^3 \cos^4 \alpha (3 — 2 \cos^2 \alpha) = \frac{1}{2} \cdot \frac{4}{3}\pi R^3\). Сокращая \(\frac{4}{3}\pi R^3\), получаем \(\cos^4 \alpha (3 — 2 \cos^2 \alpha) = \frac{1}{2}\). Пусть \(x = \cos^2 \alpha\). Уравнение принимает вид \(x^2 (3 — 2x) = \frac{1}{2}\), или \(3x^2 — 2x^3 = \frac{1}{2}\), что эквивалентно \(4x^3 — 6x^2 + 1 = 0\). Проверкой убеждаемся, что \(x = \frac{1}{2}\) является корнем этого уравнения: \(4(\frac{1}{2})^3 — 6(\frac{1}{2})^2 + 1 = 4(\frac{1}{8}) — 6(\frac{1}{4}) + 1 = \frac{1}{2} — \frac{3}{2} + 1 = 0\). Так как \(x = \cos^2 \alpha\), то \(\cos^2 \alpha = \frac{1}{2}\). Поскольку \(\alpha\) является углом в прямоугольном треугольнике, \(\cos \alpha > 0\). Поэтому \(\cos \alpha = \sqrt{\frac{1}{2}}\).

\alpha = R \cos \alpha\). Since OK bisects BC, \(BC = 2 BK = 2R \cos \alpha\).
Now, substitute the expression for BC into theДан полукруг, вращением которого вокруг диаметра АВ образован шар. Поверхность, образованная вращением хорды ВС, делит шар на равные части. Необходимо найти \(\cos \angle CBA\).

Пусть R — радиус шара, а О — его центр, совпадающий с серединой диаметра АВ. Проведем перпендикуляр CD из точки С к диаметру АВ, где D лежит на АВ. Обозначим \(\angle CBA = \alpha\).

Согласно представленному решению, рассматривается объем тела, полученного вращением области BNCD вокруг оси АВ, где BNC — дуга окружности. Этот объем вычисляется как разность объема шарового сегмента с основанием, проходящим через CD, и конуса с основанием, образованным вращением CD, и вершиной в В.

Найдем длины отрезков BC, BD и DC через R и \(\alpha\). В прямоугольном треугольнике BCD имеем \(BD = BC \cos \alpha\) и \(DC = BC \sin \alpha\). Поскольку точка С лежит на окружности радиуса R с центром в О, OC = R. Треугольник OBC является равнобедренным с