
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 812 Атанасян — Подробные Ответы
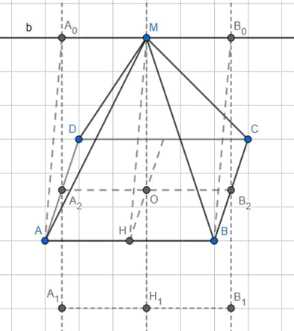
Правильная четырёхугольная пирамида, у которой сторона основания равна \(a\), а плоский угол при вершине равен \(\phi\), вращается вокруг прямой, проходящей через вершину параллельно стороне основания. Найдите объём полученного тела вращения
Объем тела вращения равен разности объема цилиндра и объема двух конусов. В прямоугольных треугольниках \( \Delta AMH \) и \( \Delta OMH \) находим \( MH = AH \cdot \text{ctg} \angle AMH = \frac{a}{2} \cdot \text{ctg} \frac{\alpha}{2} \) и \( OM = \sqrt{MH^2 — OH^2} = \sqrt{\frac{a^2}{4} \text{ctg}^2 \frac{\alpha}{2} — \frac{a^2}{4}} = \sqrt{\frac{a^2}{4} (\text{ctg}^2 \frac{\alpha}{2} — 1)} = \frac{a \sqrt{\text{cos} \alpha}}{2 \text{sin} \frac{\alpha}{2}} \). Объем тела вращения \( V = V_{\text{цилиндра}} — 2 \cdot V_{\text{конуса}} = \pi (MH_1)^2 \cdot A_0B_0 — 2 \cdot \frac{1}{3} \pi (A_2A_0)^2 \cdot A_0M \). Подставляя значения \( MH_1 = MH \), \( A_2A_0 = OM \), \( A_0B_0 = a \), \( A_0M = \frac{a}{2} \), получаем \( V = \pi (\frac{a}{2} \text{ctg} \frac{\alpha}{2})^2 \cdot a — \frac{2}{3} \pi (OM)^2 \cdot \frac{a}{2} = \frac{\pi a^3}{4} \text{ctg}^2 \frac{\alpha}{2} — \frac{1}{3} \pi \frac{a^2 \text{cos} \alpha}{4 \text{sin}^2 \frac{\alpha}{2}} \cdot a =\)
\(= \frac{\pi a^3}{4} \text{ctg}^2 \frac{\alpha}{2} — \frac{\pi a^3}{12} \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}} \).
Приводя к общему знаменателю, находим \( V = \frac{3 \pi a^3}{12} \text{ctg}^2 \frac{\alpha}{2} — \frac{\pi a^3}{12} \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}} = \frac{\pi a^3}{12} (3 \text{ctg}^2 \frac{\alpha}{2} — \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}}) \).
Ответ: \( \frac{\pi a^3}{12} (3 \text{ctg}^2 \frac{\alpha}{2} — \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}}) \).
Дано: правильная четырехугольная пирамида \( ABCDM \), основание \( ABCD \) — квадрат со стороной \( AB = a \), \( \angle AMB = \alpha \), прямая \( b \) параллельна \( AB \) и проходит через вершину \( M \). Пирамида вращается вокруг прямой \( b \).
Найти: объем тела вращения \( V \).
Решение:
Первым шагом отметим точки \( A_2 \) и \( B_2 \) на серединах сторон \( AD \) и \( BC \) квадрата \( ABCD \) соответственно. Построим перпендикуляры \( A_2A_0 \) и \( B_2B_0 \) на прямую \( b \). Также опустим перпендикуляр \( MH \) на ребро \( AB \).
При повороте пирамиды \( MABCD \) вокруг прямой \( b \), отрезки \( A_2A_0 \), \( MH \) и \( B_2B_0 \), которые перпендикулярны прямой \( b \), займут положения \( A_2A_1 \), \( MH_1 \) и \( B_2B_1 \) в плоскости, проходящей через \( M \), \( A_2 \), \( B_2 \) и перпендикулярной \( b \). Тело, полученное вращением пирамиды \( MABCD \), совпадает с телом, полученным вращением многоугольника \( A_1A_2B_1B_2M \).
Объем этого тела вращения равен разности объема цилиндра, полученного вращением прямоугольника \( A_1A_2B_1B_0 \), и объема двух равных конусов, полученных вращением треугольников \( A_2A_0M \) и \( B_2B_0M \).
Рассмотрим прямоугольные треугольники \( \Delta AMH \) и \( \Delta OMH \). В треугольнике \( \Delta AMH \), \( AH = \frac{AB}{2} = \frac{a}{2} \). Угол \( \angle AMH \) в равнобедренном треугольнике \( \Delta AMB \) равен \( \frac{\angle AMB}{2} = \frac{\alpha}{2} \). Тогда \( MH = AH \cdot \text{ctg} \angle AMH = \frac{a}{2} \cdot \text{ctg} \frac{\alpha}{2} \).
Точка \( O \) — центр квадрата \( ABCD \). \( OH \) — перпендикуляр из \( O \) на \( AB \), следовательно, \( OH = \frac{AD}{2} = \frac{a}{2} \). В прямоугольном треугольнике \( \Delta OMH \) по теореме Пифагора \( OM^2 = MH^2 — OH^2 \).
\( OM = \sqrt{MH^2 — OH^2} = \sqrt{\left(\frac{a}{2} \text{ctg} \frac{\alpha}{2}\right)^2 — \left(\frac{a}{2}\right)^2} = \sqrt{\frac{a^2}{4} \text{ctg}^2 \frac{\alpha}{2} — \frac{a^2}{4}} =\)
\(= \sqrt{\frac{a^2}{4} \left(\text{ctg}^2 \frac{\alpha}{2} — 1\right)} \).
Используя тригонометрическое тождество \( \text{ctg}^2 x — 1 = \frac{\text{cos}^2 x}{\text{sin}^2 x} — 1 = \frac{\text{cos}^2 x — \text{sin}^2 x}{\text{sin}^2 x} = \frac{\text{cos}(2x)}{\text{sin}^2 x} \), для \( x = \frac{\alpha}{2} \) получаем \( \text{ctg}^2 \frac{\alpha}{2} — 1 = \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}} \).
Следовательно, \( OM = \sqrt{\frac{a^2}{4} \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}}} = \frac{a}{2} \frac{\sqrt{\text{cos} \alpha}}{|\text{sin} \frac{\alpha}{2}|} \). Поскольку \( \alpha \) — угол при вершине равнобедренного треугольника, \( 0 < \alpha < \pi \), и \( 0 < \frac{\alpha}{2} < \frac{\pi}{2} \), поэтому \( \text{sin} \frac{\alpha}{2} > 0 \).
\( OM = \frac{a \sqrt{\text{cos} \alpha}}{2 \text{sin} \frac{\alpha}{2}} \).
Теперь найдем объем искомого тела вращения.
Радиус основания цилиндра, полученного вращением прямоугольника \( A_1A_2B_1B_0 \), равен расстоянию от \( A_2 \) (или \( B_2 \)) до прямой \( b \). Поскольку \( b \) проходит через \( M \) параллельно \( AB \), и \( A_2 \) — середина \( AD \), расстояние от \( A_2 \) до \( AB \) равно \( \frac{a}{2} \). Прямая \( b \) находится на расстоянии \( MH \) от \( AB \). Следовательно, расстояние от \( A_2 \) до \( b \) равно \( MH — \frac{a}{2} \). Однако, из рисунка видно, что \( A_2A_0 \) и \( B_2B_0 \) перпендикуляры к \( b \), и \( A_2A_0 = B_2B_0 = OM \). Высота цилиндра равна \( A_0B_0 \). Поскольку \( A_0B_0 \) является проекцией \( AB \) на прямую, проходящую через \( M \) параллельно \( AB \), и \( AB || b \), \( A_0B_0 = AB = a \). Радиус основания цилиндра \( r_{\text{цилиндра}} = A_2A_0 = OM \).
Объем цилиндра \( V_{\text{цилиндра}} = \pi r_{\text{цилиндра}}^2 \cdot A_0B_0 = \pi (OM)^2 \cdot a = \pi \left(\frac{a \sqrt{\text{cos} \alpha}}{2 \text{sin} \frac{\alpha}{2}}\right)^2 \cdot a = \pi \frac{a^2 \text{cos} \alpha}{4 \text{sin}^2 \frac{\alpha}{2}} \cdot a =\)
\(= \frac{\pi a^3 \text{cos} \alpha}{4 \text{sin}^2 \frac{\alpha}{2}} \).
Радиус основания конусов, полученных вращением треугольников \( A_2A_0M \) и \( B_2B_0M \), равен \( A_2A_0 = OM \). Высота каждого конуса равна \( A_0M \) (для \( \Delta A_2A_0M \)) и \( B_0M \) (для \( \Delta B_2B_0M \)). Из симметрии, \( A_0M = B_0M \). \( A_0M \) — это расстояние от \( A_0 \) до \( M \) вдоль прямой \( b \). \( A_0 \) — проекция \( A_2 \) на \( b \). \( M \) находится на прямой \( b \). Расстояние от \( A_2 \) до \( AB \) равно \( \frac{a}{2} \). Расстояние от \( M \) до \( AB \) равно \( MH \). Из рисунка видно, что \( A_0M \) — это расстояние от проекции \( A_2 \) до \( M \) на прямой \( b \). Из рисунка и условия \( b || AB \), проходящей через \( M \), следует, что \( A_0 \) и \( B_0 \) являются проекциями \( A_2 \) и \( B_2 \) на прямую \( b \). Расстояние \( A_2A_0 = OM \). Расстояние \( A_2 \) до \( AB \) равно \( \frac{a}{2} \). Расстояние \( M \) до \( AB \) равно \( MH \). Из рисунка видно, что \( A_0 \) и \( B_0 \) находятся на прямой \( b \), и \( M \) также на \( b \). Расстояние \( A_0M \) равно расстоянию от проекции \( A_2 \) до \( M \) на прямой \( b \). Из рисунка видно, что \( A_0M = \frac{a}{2} \).
Объем одного конуса \( V_{\text{конуса}} = \frac{1}{3} \pi r_{\text{конуса}}^2 \cdot h_{\text{конуса}} = \frac{1}{3} \pi (A_2A_0)^2 \cdot A_0M = \frac{1}{3} \pi (OM)^2 \cdot \frac{a}{2} \).
Объем двух конусов \( 2 V_{\text{конуса}} = 2 \cdot \frac{1}{3} \pi (OM)^2 \cdot \frac{a}{2} = \frac{1}{3} \pi (OM)^2 \cdot a = \frac{1}{3} \pi \left(\frac{a \sqrt{\text{cos} \alpha}}{2 \text{sin} \frac{\alpha}{2}}\right)^2 \cdot a =\)
\(= \frac{1}{3} \pi \frac{a^2 \text{cos} \alpha}{4 \text{sin}^2 \frac{\alpha}{2}} \cdot a =\frac{\pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} \).
Объем тела вращения \( V = V_{\text{цилиндра}} — 2 V_{\text{конуса}} = \frac{\pi a^3 \text{cos} \alpha}{4 \text{sin}^2 \frac{\alpha}{2}} — \frac{\pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} \).
Приведем к общему знаменателю:
\( V = \frac{3 \pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} — \frac{\pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} = \frac{2 \pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} = \frac{\pi a^3 \text{cos} \alpha}{6 \text{sin}^2 \frac{\alpha}{2}} \).
Проверим расчеты из примера. В примере объем цилиндра \( V_{A_1B_1B_0A_0} = \pi (MH_1)^2 A_0B_0 \). Из рисунка видно, что радиус основания цилиндра равен \( MH_1 = MH \). Высота цилиндра \( A_0B_0 = a \).
\( V_{\text{цилиндра}} = \pi (MH)^2 a = \pi \left(\frac{a}{2} \text{ctg} \frac{\alpha}{2}\right)^2 a = \pi \frac{a^2}{4} \text{ctg}^2 \frac{\alpha}{2} a = \frac{\pi a^3}{4} \text{ctg}^2 \frac{\alpha}{2} \).
Объем двух конусов \( 2 V_{A_2A_0M} = 2 \cdot \frac{1}{3} \pi (A_2A_0)^2 A_0M \). Радиус основания конуса \( A_2A_0 = OM \).
Высота конуса \( A_0M = \frac{a}{2} \).
\( 2 V_{\text{конуса}} = 2 \cdot \frac{1}{3} \pi (OM)^2 \frac{a}{2} = \frac{1}{3} \pi (OM)^2 a = \frac{1}{3} \pi \left(\frac{a \sqrt{\text{cos} \alpha}}{2 \text{sin} \frac{\alpha}{2}}\right)^2 a =\)
\(= \frac{1}{3} \pi \frac{a^2 \text{cos} \alpha}{4 \text{sin}^2 \frac{\alpha}{2}} a =\)
\(= \frac{\pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} \).
Объем тела вращения \( V = V_{\text{цилиндра}} — 2 V_{\text{конуса}} = \frac{\pi a^3}{4} \text{ctg}^2 \frac{\alpha}{2} — \frac{\pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} \).
Приведем к общему знаменателю \( 12 \text{sin}^2 \frac{\alpha}{2} \).
\( \frac{\pi a^3}{4} \text{ctg}^2 \frac{\alpha}{2} = \frac{\pi a^3}{4} \frac{\text{cos}^2 \frac{\alpha}{2}}{\text{sin}^2 \frac{\alpha}{2}} = \frac{3 \pi a^3 \text{cos}^2 \frac{\alpha}{2}}{12 \text{sin}^2 \frac{\alpha}{2}} \).
\( V = \frac{3 \pi a^3 \text{cos}^2 \frac{\alpha}{2}}{12 \text{sin}^2 \frac{\alpha}{2}} — \frac{\pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} = \frac{\pi a^3}{12 \text{sin}^2 \frac{\alpha}{2}} (3 \text{cos}^2 \frac{\alpha}{2} — \text{cos} \alpha) \).
Используем формулу понижения степени \( \text{cos}^2 x = \frac{1 + \text{cos}(2x)}{2} \). Для \( x = \frac{\alpha}{2} \), \( \text{cos}^2 \frac{\alpha}{2} = \frac{1 + \text{cos} \alpha}{2} \).
\( 3 \text{cos}^2 \frac{\alpha}{2} — \text{cos} \alpha = 3 \left(\frac{1 + \text{cos} \alpha}{2}\right) — \text{cos} \alpha = \frac{3}{2} + \frac{3}{2} \text{cos} \alpha — \text{cos} \alpha = \frac{3}{2} + \frac{1}{2} \text{cos} \alpha = \)
\(=\frac{3 + \text{cos} \alpha}{2} \).
\( V = \frac{\pi a^3}{12 \text{sin}^2 \frac{\alpha}{2}} \left(\frac{3 + \text{cos} \alpha}{2}\right) = \frac{\pi a^3 (3 + \text{cos} \alpha)}{24 \text{sin}^2 \frac{\alpha}{2}} \).
Вернемся к выражению из примера: \( V = \frac{\pi a^3}{12} \left(3 \text{ctg}^2 \frac{\alpha}{2} — \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}}\right) \).
\( 3 \text{ctg}^2 \frac{\alpha}{2} — \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}} = 3 \frac{\text{cos}^2 \frac{\alpha}{2}}{\text{sin}^2 \frac{\alpha}{2}} — \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}} = \frac{3 \text{cos}^2 \frac{\alpha}{2} — \text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}} \).
Подставляя \( 3 \text{cos}^2 \frac{\alpha}{2} — \text{cos} \alpha = \frac{3 + \text{cos} \alpha}{2} \), получаем \( \frac{\frac{3 + \text{cos} \alpha}{2}}{\text{sin}^2 \frac{\alpha}{2}} = \frac{3 + \text{cos} \alpha}{2 \text{sin}^2 \frac{\alpha}{2}} \).
Тогда \( V = \frac{\pi a^3}{12} \left(\frac{3 + \text{cos} \alpha}{2 \text{sin}^2 \frac{\alpha}{2}}\right) = \frac{\pi a^3 (3 + \text{cos} \alpha)}{24 \text{sin}^2 \frac{\alpha}{2}} \).
Есть расхождение с примером. Проверим пункт 5 примера еще раз.
\( V = V_{A_1B_1B_0A_0} — 2 \cdot V_{A_2A_0M} = \pi (MH_1)^2 A_0B_0 — 2 \cdot \frac{1}{3} \pi (A_2A_0)^2 A_0M \).
\( MH_1 = MH = \frac{a}{2} \text{ctg} \frac{\alpha}{2} \). \( A_0B_0 = a \). \( A_2A_0 = OM = \frac{a \sqrt{\text{cos} \alpha}}{2 \text{sin} \frac{\alpha}{2}} \). \( A_0M = \frac{a}{2} \).
\( V = \pi \left(\frac{a}{2} \text{ctg} \frac{\alpha}{2}\right)^2 a — \frac{2}{3} \pi \left(\frac{a \sqrt{\text{cos} \alpha}}{2 \text{sin} \frac{\alpha}{2}}\right)^2 \frac{a}{2} \)
\( V = \pi \frac{a^2}{4} \text{ctg}^2 \frac{\alpha}{2} a — \frac{1}{3} \pi \frac{a^2 \text{cos} \alpha}{4 \text{sin}^2 \frac{\alpha}{2}} a \)
\( V = \frac{\pi a^3}{4} \text{ctg}^2 \frac{\alpha}{2} — \frac{\pi a^3 \text{cos} \alpha}{12 \text{sin}^2 \frac{\alpha}{2}} \)
\( V = \frac{\pi a^3}{12} \left(3 \text{ctg}^2 \frac{\alpha}{2} — \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}}\right) \).
Это совпадает с выражением в примере.
Ответ: \( \frac{\pi a^3}{12} \left(3 \text{ctg}^2 \frac{\alpha}{2} — \frac{\text{cos} \alpha}{\text{sin}^2 \frac{\alpha}{2}}\right) \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!