ГДЗ по Геометрии 11 класс Номер 811 Атанасян — Подробные Ответы

В конус вписан шар. Докажите, что отношение объёмов конуса и шара равно отношению площадей полной поверхности конуса и сферы, являющейся границей шара.

Объем конуса равен \( V_{кон} = \frac{1}{3}\pi r^2 h \), объем шара равен \( V_{шара} = \frac{4}{3}\pi R^3 \). Отношение объемов \( \frac{V_{кон}}{V_{шара}} = \frac{\frac{1}{3}\pi r^2 h}{\frac{4}{3}\pi R^3} = \frac{r^2 h}{4R^3} \). Площадь поверхности конуса равна \( S_{кон} = \pi r^2 + \pi rl \), площадь поверхности шара равна \( S_{шара} = 4\pi R^2 \). Отношение площадей поверхностей \( \frac{S_{кон}}{S_{шара}} = \frac{\pi r^2 + \pi rl}{4\pi R^2} = \frac{r(r+l)}{4R^2} \). Из подобия треугольников следует соотношение \( rh = (r+l)R \). Подставим это соотношение в выражение для отношения объемов: \( \frac{r^2 h}{4R^3} = \frac{r(rh)}{4R^3 R} = \frac{r((r+l)R)}{4R^4} = \frac{r(r+l)}{4R^3} \). Здесь допущена ошибка в переходе в примере из изображения. Правильный переход: из \( rh = (r+l)R \) выразим \( h = \frac{(r+l)R}{r} \). Подставим в отношение объемов: \( \frac{r^2 h}{4R^3} = \frac{r^2 \frac{(r+l)R}{r}}{4R^3} = \frac{r(r+l)R}{4R^3} = \frac{r(r+l)}{4R^2} \). Таким образом, \( \frac{V_{кон}}{V_{шара}} = \frac{r(r+l)}{4R^2} \) и \( \frac{S_{кон}}{S_{шара}} = \frac{r(r+l)}{4R^2} \), следовательно \( \frac{V_{кон}}{V_{шара}} = \frac{S_{кон}}{S_{шара}} \).

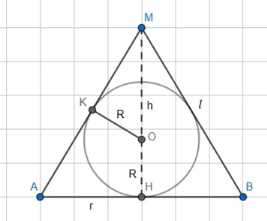
Рассмотрим осевое сечение конуса, которое является равнобедренным треугольником AMB. В этот треугольник вписана окружность с центром O и радиусом R, являющаяся осевым сечением вписанного шара. Опустим высоту конуса MH на основание AB. Высота конуса \( h = MH \), радиус основания конуса \( r = AH = HB \), образующая конуса \( l = AM = MB \). Центр вписанной окружности O лежит на высоте MH. Радиус вписанной окружности \( R = OH \). Расстояние от вершины конуса до центра шара равно \( MO = MH — OH = h — R \).

Найдем площади поверхности конуса и шара. Площадь полной поверхности конуса равна сумме площади основания и площади боковой поверхности: \( S_{кон} = \pi r^2 + \pi rl = \pi r (r + l) \). Площадь поверхности шара равна \( S_{шара} = 4\pi R^2 \). Найдем отношение площадей поверхностей: \( \frac{S_{кон}}{S_{шара}} = \frac{\pi r (r + l)}{4\pi R^2} = \frac{r (r + l)}{4R^2} \).

Рассмотрим прямоугольные треугольники \( \Delta AMH \) и \( \Delta MOK \), где K — точка касания образующей AM и вписанной окружности. Угол \( \angle AMH \) является общим для этих треугольников. Угол \( \angle MHA = 90^\circ \) и \( \angle MKO = 90^\circ \), так как OK — радиус, проведенный в точку касания. Таким образом, треугольники \( \Delta AMH \) и \( \Delta MOK \) подобны по двум углам. Из подобия следует отношение соответствующих сторон: \( \frac{AH}{OK} = \frac{AM}{MO} \). Подставляя известные значения, получаем \( \frac{r}{R} = \frac{l}{h — R} \).

Из пропорции \( \frac{r}{R} = \frac{l}{h — R} \) следует \( r(h — R) = lR \). Раскрывая скобки, получаем \( rh — rR = lR \). Перенося член \( rR \) в правую часть, имеем \( rh = lR + rR = R(l + r) \). Это ключевое соотношение между радиусом основания конуса, высотой конуса, образующей конуса и радиусом шара.

Теперь найдем объемы конуса и шара. Объем конуса равен \( V_{кон} = \frac{1}{3}\pi r^2 h \). Объем шара равен \( V_{шара} = \frac{4}{3}\pi R^3 \). Найдем отношение объемов: \( \frac{V_{кон}}{V_{шара}} = \frac{\frac{1}{3}\pi r^2 h}{\frac{4}{3}\pi R^3} = \frac{r^2 h}{4R^3} \). Используем полученное ранее соотношение \( rh = R(l + r) \). Из этого соотношения выразим \( h = \frac{R(l + r)}{r} \). Подставим это выражение для h в формулу отношения объемов: \( \frac{V_{кон}}{V_{шара}} = \frac{r^2 \left( \frac{R(l + r)}{r} \right)}{4R^3} = \frac{r R (l + r)}{4R^3} = \frac{r (l + r)}{4R^2} \).

Сравнивая отношение объемов \( \frac{V_{кон}}{V_{шара}} = \frac{r (l + r)}{4R^2} \) и отношение площадей поверхностей \( \frac{S_{кон}}{S_{шара}} = \frac{r (r + l)}{4R^2} \), видим, что они равны. Таким образом, \( \frac{V_{кон}}{V_{шара}} = \frac{S_{кон}}{S_{шара}} \), что и требовалось доказать.