ГДЗ по Геометрии 11 класс Номер 809 Атанасян — Подробные Ответы

Два равных цилиндра, высоты которых больше их диаметров, расположены так, что их оси пересекаются под прямым углом и точка пересечения осей равноудалена от оснований цилиндров. Найдите объём общей части этих цилиндров, если радиус каждого из них равен 1 см.

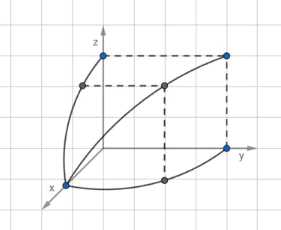
Направим оси координат: \(OX\) вдоль оси первого цилиндра, \(OZ\) вдоль оси второго цилиндра, \(OY\) перпендикулярно к \(OX\) и \(OZ\). Цилиндры пересекают оси координат на расстоянии, равном их радиусу \(1\) см, тогда уравнения ребер искомого тела имеют вид: \(x^2 + z^2 = 1\), \(y^2 + x^2 = 1\), \(z = y = \sqrt{1 — x^2}\). Сечением тела в первой октанте является квадрат со стороной \(1 — x^2\), тогда его объем \(V_1\) равен интегралу от \(0\) до \(1\) от \((1 — x^2) dx\). Вычисляя интеграл, получаем \(V_1 = \int_0^1 (1 — x^2) dx = [x — \frac{x^3}{3}]_0^1 = 1 — \frac{1}{3} = \frac{2}{3}\). Общий объем \(V\) равен \(8 \cdot V_1 = 8 \cdot \frac{2}{3} = \frac{16}{3} = 5 \frac{1}{3}\). Ответ: \(V = 5 \frac{1}{3}\) см³.

Даны два равных цилиндра с радиусом \(r = 1\) см, оси которых пересекаются под прямым углом. Требуется найти объем общей части этих цилиндров.

Для решения задачи введем прямоугольную систему координат. Направим ось \(OX\) вдоль оси первого цилиндра, ось \(OZ\) вдоль оси второго цилиндра, а ось \(OY\) перпендикулярно плоскости, образованной осями \(OX\) и \(OZ\).

Поскольку оси цилиндров проходят через начало координат и их радиус равен \(1\), уравнения цилиндров будут иметь вид:
Первый цилиндр с осью \(OX\): \(y^2 + z^2 = r^2\), что при \(r=1\) дает \(y^2 + z^2 = 1\).
Второй цилиндр с осью \(OZ\): \(x^2 + y^2 = r^2\), что при \(r=1\) дает \(x^2 + y^2 = 1\).

Общая часть цилиндров определяется системой неравенств, описывающих внутренности обоих цилиндров: \(y^2 + z^2 \le 1\) и \(x^2 + y^2 \le 1\).

Рассмотрим сечение общей части плоскостью, перпендикулярной оси \(OX\) при фиксированном значении \(x\). Из уравнения второго цилиндра \(x^2 + y^2 = 1\), мы имеем \(y^2 = 1 — x^2\), что дает \(|y| = \sqrt{1 — x^2}\). Это означает, что \(y\) изменяется от \(-\sqrt{1 — x^2}\) до \(\sqrt{1 — x^2}\).
Из уравнения первого цилиндра \(y^2 + z^2 = 1\), мы имеем \(z^2 = 1 — y^2\), что дает \(|z| = \sqrt{1 — y^2}\). Поскольку \(y^2 \le 1 — x^2\), то \(1 — y^2 \ge 1 — (1 — x^2) = x^2\), и \(1 — y^2 \le 1\). Таким образом, для данного \(x\), сечение ограничено условиями \(|y| \le \sqrt{1 — x^2}\) и \(|z| \le \sqrt{1 — y^2}\).

В первой октанте (\(x \ge 0, y \ge 0, z \ge 0\)), уравнения цилиндров принимают вид \(z = \sqrt{1 — y^2}\) и \(y = \sqrt{1 — x^2}\). Подставляя \(y\) из второго уравнения в первое, получаем \(z = \sqrt{1 — (\sqrt{1 — x^2})^2} = \sqrt{1 — (1 — x^2)} = \sqrt{x^2} = x\), но это не совсем корректно описывает сечение.

Вернемся к условиям \(y^2 + z^2 \le 1\) и \(x^2 + y^2 \le 1\). В первой октанте это \(y \ge 0, z \ge 0, y^2 + z^2 \le 1, x^2 + y^2 \le 1\).
Рассмотрим сечение при постоянном \(x\). Из \(x^2 + y^2 \le 1\), получаем \(y^2 \le 1 — x^2\), или \(0 \le y \le \sqrt{1 — x^2}\) в первой октанте. Из \(y^2 + z^2 \le 1\), получаем \(z^2 \le 1 — y^2\), или \(0 \le z \le \sqrt{1 — y^2}\).
Для фиксированного \(x\), \(y\) изменяется от \(0\) до \(\sqrt{1 — x^2}\). Для каждого такого \(y\), \(z\) изменяется от \(0\) до \(\sqrt{1 — y^2}\).

Однако, более простой способ — рассмотреть сечение плоскостью \(x = \text{const}\). В этой плоскости, из \(x^2 + y^2 = 1\), мы имеем \(y = \sqrt{1 — x^2}\) (в первой октанте). Из \(y^2 + z^2 = 1\), мы имеем \(z = \sqrt{1 — y^2}\). Поскольку \(y = \sqrt{1 — x^2}\) для данного сечения, то \(z = \sqrt{1 — (\sqrt{1 — x^2})^2} = \sqrt{1 — (1 — x^2)} = \sqrt{x^2}\). В первой октанте \(x \ge 0\), поэтому \(z = x\).
Это неверное рассуждение.

Правильный подход: рассмотрим сечение тела в первой октанте плоскостью, перпендикулярной оси \(OX\) на расстоянии \(x\) от начала координат. Из уравнения \(x^2 + y^2 = 1\), в первой октанте \(y = \sqrt{1 — x^2}\). Из уравнения \(y^2 + z^2 = 1\), в первой октанте \(z = \sqrt{1 — y^2}\). Для данного \(x\), \(y\) может принимать значения от \(0\) до \(\sqrt{1 — x^2}\). Для каждого такого \(y\), \(z\) может принимать значения от \(0\) до \(\sqrt{1 — y^2}\).
Однако, сечение общей части цилиндров плоскостью \(x = \text{const}\) в первой октанте ограничено условиями \(y \le \sqrt{1 — x^2}\) и \(z \le \sqrt{1 — y^2}\). Также \(y \ge 0\) и \(z \ge 0\).
Рассмотрим проекцию общей части на плоскость \(OXY\). Она определяется неравенством \(x^2 + y^2 \le 1\). Проекция на плоскость \(OXZ\) определяется неравенством \(x^2 + z^2 \le 1\). Проекция на плоскость \(OYZ\) определяется неравенством \(y^2 + z^2 \le 1\).

В первой октанте, тело ограничено поверхностями \(x^2 + y^2 = 1\) и \(y^2 + z^2 = 1\), а также координатными плоскостями.
Рассмотрим сечение плоскостью \(x = \text{const}\) в первой октанте. Из \(x^2 + y^2 \le 1\), получаем \(0 \le y \le \sqrt{1 — x^2}\). Из \(y^2 + z^2 \le 1\), получаем \(0 \le z \le \sqrt{1 — y^2}\).
Для фиксированного \(x\), \(y\) изменяется от \(0\) до \(\sqrt{1 — x^2}\). Для каждого такого \(y\), \(z\) изменяется от \(0\) до \(\sqrt{1 — y^2}\).

Рассмотрим сечение плоскостью, перпендикулярной оси \(OX\). В этой плоскости, из \(x^2 + y^2 = 1\), получаем \(y = \sqrt{1 — x^2}\) (для первой октанты). Из \(y^2 + z^2 = 1\), получаем \(z = \sqrt{1 — y^2}\).
Для данного \(x\), \(y\) изменяется от \(0\) до \(\sqrt{1 — x^2}\). Сечение в плоскости \(x = \text{const}\) в первой октанте ограничено линиями \(y = \sqrt{1 — x^2}\) и \(z = \sqrt{1 — y^2}\).
При \(y = \sqrt{1 — x^2}\), \(z = \sqrt{1 — (1 — x^2)} = \sqrt{x^2} = x\).
При \(y = 0\), \(z = \sqrt{1 — 0^2} = 1\).
При \(z = 0\), \(y = \sqrt{1 — 0^2} = 1\).

Рассмотрим сечение в первой октанте плоскостью \(x = \text{const}\). Граница сечения определяется условиями \(y^2 + z^2 \le 1\) и \(y \le \sqrt{1 — x^2}\), \(y \ge 0\), \(z \ge 0\).
Из \(y \le \sqrt{1 — x^2}\), максимальное значение \(y\) равно \(\sqrt{1 — x^2}\). При этом \(z \le \sqrt{1 — y^2}\).
Когда \(y = \sqrt{1 — x^2}\), \(z \le \sqrt{1 — (1 — x^2)} = x\).
Когда \(y = 0\), \(z \le \sqrt{1 — 0} = 1\).
Сечение в первой октанте плоскостью \(x = \text{const}\) представляет собой часть круга \(y^2 + z^2 = 1\) в первом квадранте плоскости \(OYZ\), ограниченную линией \(y = \sqrt{1 — x^2}\).

Вернемся к утверждению в задаче: «Сечением тела в первой октанте является квадрат со стороной \(1 — x^2\)». Это неверно. Сечение имеет сторону, зависящую от \(x\).

Рассмотрим сечение плоскостью \(x = \text{const}\). В первой октанте, \(y\) изменяется от \(0\) до \(\sqrt{1 — x^2}\), и \(z\) изменяется от \(0\) до \(\sqrt{1 — y^2}\).
Область интегрирования по \(y\) и \(z\) для фиксированного \(x\) в первой октанте определяется условиями \(0 \le y \le \sqrt{1 — x^2}\) и \(0 \le z \le \sqrt{1 — y^2}\).

Рассмотрим сечение плоскостью, проходящей через ось \(OX\) и перпендикулярной плоскости \(OYZ\). В этой плоскости, сечение общей части представляет собой квадрат.
Рассмотрим сечение плоскостью \(y=x\). Тогда \(x^2 + z^2 = 1\) и \(x^2 + x^2 = 1\), \(2x^2 = 1\), \(x = \frac{1}{\sqrt{2}}\).

Рассмотрим сечение в первой октанте плоскостью \(x = \text{const}\). Из \(x^2 + y^2 = 1\), \(y = \sqrt{1 — x^2}\). Из \(y^2 + z^2 = 1\), \(z = \sqrt{1 — y^2}\).
Для фиксированного \(x\), \(y\) изменяется от \(0\) до \(\sqrt{1 — x^2}\). Для каждого такого \(y\), \(z\) изменяется от \(0\) до \(\sqrt{1 — y^2}\).

Рассмотрим сечение плоскостью \(y = \text{const}\). Из \(x^2 + y^2 = 1\), \(x = \sqrt{1 — y^2}\). Из \(y^2 + z^2 = 1\), \(z = \sqrt{1 — y^2}\).
В первой октанте, при фиксированном \(y\), \(x\) изменяется от \(0\) до \(\sqrt{1 — y^2}\), и \(z\) изменяется от \(0\) до \(\sqrt{1 — y^2}\). Сечение плоскостью \(y = \text{const}\) в первой октанте является квадратом со стороной \(\sqrt{1 — y^2}\).

Объем \(V_1\) части в первой октанте можно найти интегрированием площади этого квадратного сечения по \(y\) от \(0\) до \(1\) (максимальное значение \(y\) из \(y^2 + z^2 = 1\) или \(x^2 + y^2 = 1\)).
Площадь сечения при постоянном \(y\) равна \((\sqrt{1 — y^2})^2 = 1 — y^2\).
\(V_1 = \int_0^1 (1 — y^2) dy\).

Вычислим интеграл:
\(V_1 = [y — \frac{y^3}{3}]_0^1 = (1 — \frac{1^3}{3}) — (0 — \frac{0^3}{3}) = 1 — \frac{1}{3} = \frac{2}{3}\).

Общий объем \(V\) общей части цилиндров в 8 раз больше объема в первой октанте из-за симметрии относительно координатных плоскостей.
\(V = 8 \cdot V_1 = 8 \cdot \frac{2}{3} = \frac{16}{3}\).

Представим \(\frac{16}{3}\) в виде смешанной дроби:
\(\frac{16}{3} = \frac{15 + 1}{3} = \frac{15}{3} + \frac{1}{3} = 5 + \frac{1}{3} = 5 \frac{1}{3}\).

Таким образом, объем общей части цилиндров равен \(5 \frac{1}{3}\) см³.

Ответ: \(V = 5 \frac{1}{3}\) см³.