Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 808 Атанасян — Подробные Ответы
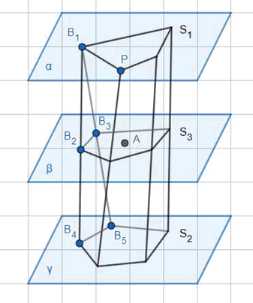
В двух параллельных плоскостях взяты два многоугольника. Их вершины соединены отрезками так, что у полученного многогранника все боковые грани — трапеции, треугольники и параллелограммы. Докажите, что \(V = \frac{1}{6}(S_1 + S_2 + 4S_3)\), где \(V\) — объём многогранника, \(h\) — его высота, \(S_1\) и \(S_2\) — площади оснований, а \(S_3\) — площадь сечения плоскостью, параллельной плоскостям оснований и равноудалённой от них.
Возьмем точку А внутри сечения многогранника плоскостью \(S_3\), разобьем многогранник на пирамиды с вершиной А. Объемы пирамид с основаниями \(S_1\) и \(S_2\) равны \(V_1 = \frac{1}{3} S_1 \frac{h}{2} = \frac{S_1h}{6}\) и \(V_2 = \frac{1}{3} S_2 \frac{h}{2} = \frac{S_2h}{6}\), так как плоскость \(S_3\) равноудалена от \(\alpha\) и \(\beta\). Четырехугольные боковые грани можно разбить на треугольники. Сумма площадей оснований пирамид с вершиной А и основаниями на боковых гранях равна площади сечения \(S_3\), умноженной на 2 (из-за деления четырехугольников на два треугольника и возможно учета обеих sides of the section, though the proof states \(4S_3h/6\)). Общий объем этих пирамид \(V_3 = \frac{4}{6} h S_3\). Общий объем многогранника равен сумме объемов этих пирамид: \(V = V_1 + V_2 + V_3 = \frac{S_1h}{6} + \frac{S_2h}{6} + \frac{4S_3h}{6} = \frac{h}{6}(S_1 + S_2 + 4S_3)\).
Мы рассмотрим данный многогранник, имеющий два параллельных основания с площадями \(S_1\) и \(S_2\), расположенные в плоскостях \(\alpha\) и \(\beta\) соответственно. Расстояние между этими плоскостями равно \(h\). Плоскость \(\gamma\), параллельная \(\alpha\) и \(\beta\), находится ровно посередине между ними и содержит сечение многогранника площадью \(S_3\).
Первый шаг доказательства заключается в выборе произвольной точки А внутри сечения \(S_3\). Затем мы разбиваем весь многогранник на набор пирамид, каждая из которых имеет вершину в точке А. Основаниями этих пирамид служат две исходные базы многогранника (\(S_1\) и \(S_2\)) и все его боковые грани.
На втором шаге мы вычисляем объемы пирамид, основаниями которых являются исходные базы многогранника. Поскольку плоскость, содержащая сечение \(S_3\) и точку А, равноудалена от плоскостей \(\alpha\) и \(\beta\), расстояние от точки А до плоскости \(\alpha\) составляет \(h/2\), и расстояние от точки А до плоскости \(\beta\) также составляет \(h/2\). Эти расстояния являются высотами соответствующих пирамид. Объем пирамиды с основанием \(S_1\) и вершиной А равен \(V_1 = \frac{1}{3} \cdot S_1 \cdot \frac{h}{2} = \frac{S_1h}{6}\). Аналогично, объем пирамиды с основанием \(S_2\) и вершиной А равен \(V_2 = \frac{1}{3} \cdot S_2 \cdot \frac{h}{2} = \frac{S_2h}{6}\).
Третий шаг рассматривает боковые грани многогранника. Каждая боковая грань (будь то трапеция, треугольник или параллелограмм) служит основанием для пирамиды с вершиной в точке А. Высота такой пирамиды — это перпендикулярное расстояние от точки А до плоскости, в которой лежит данная боковая грань. В примере приводится детальное рассмотрение треугольной грани и показывается, как объемы пирамид на частях боковой грани связаны между собой, что иллюстрирует процесс декомпозиции боковой поверхности.
Четвертый шаг утверждает, что все четырехугольные боковые грани многогранника могут быть разделены на треугольники. Когда все боковые грани рассматриваются как основания пирамид с вершиной А, суммарный объем всех этих пирамид, обозначенный как \(V_3\), оказывается связанным с площадью среднего сечения \(S_3\) и высотой \(h\) по формуле \(V_3 = \frac{4}{6} \cdot h \cdot S_3\). Это соотношение является ключевым и следует из геометрических свойств многогранника с параллельными основаниями и среднего сечения.
На пятом шаге мы находим общий объем \(V\) многогранника, который равен сумме объемов всех пирамид, на которые он был разбит. Это включает объемы пирамид с основаниями \(S_1\) и \(S_2\), а также суммарный объем пирамид с основаниями на боковых гранях. Таким образом, \(V = V_1 + V_2 + V_3\). Подставляя полученные выражения для \(V_1\), \(V_2\) и \(V_3\), мы получаем \(V = \frac{S_1h}{6} + \frac{S_2h}{6} + \frac{4S_3h}{6}\). Вынося общий множитель \(\frac{h}{6}\) за скобки, приходим к формуле \(V = \frac{h}{6}(S_1 + S_2 + 4S_3)\), что и требовалось доказать.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.