
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 807 Атанасян — Подробные Ответы
Точки E и F — середины рёбер DC и BB1 куба ABCDA1B1C1D1 с ребром 1 см. Найдите объём тетраэдра ADEF.
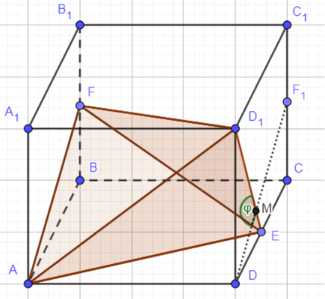
Дано: \(AA_1 = 1\) см; \(DE = EC\); \(BF = FB_1\). Найти: объем тетраэдра \(AD_1EF\). Решение: Ребра тетраэдра \(AF = a\) и \(D_1E = b\), расстояние между ними \(AD = c\). Отметим точку \(F_1\) на \(CC_1\) так, чтобы \(CF_1 = C_1F_1\) и точку \(M = D_1E \cap DF_1\), тогда \(DF_1 \parallel AF\) и углом между гранями тетраэдра \(AF\) и \(D_1E\) является \(\angle DMD_1 = \varphi\). Прямоугольные треугольники равны: \(\triangle ABF = \triangle DD_1E\). \(AB = DD_1 = 1\), \(FB = DE = \frac{1}{2}\). \(a = b = \sqrt{AB^2 + FB^2} = \sqrt{1^2 + (\frac{1}{2})^2} = \sqrt{1 + \frac{1}{4}} = \sqrt{\frac{5}{4}}\), \(c = AD = 1\). \(DD_1 = DC = 1\), \(DE = CF_1 = \frac{1}{2}\), \(\triangle DD_1E = \triangle DCF_1\). \(\angle CDF_1 = \angle DD_1E\), \(\angle D_1MD = 180^\circ — \angle DD_1E — \angle D_1DM\). \(\varphi = \angle D_1MD = 180^\circ — \angle CDF_1 — (90^\circ — \angle CDF_1) = 90^\circ\). По формуле, доказанной в задании 803: \(V_{тетр} = \frac{abc \cdot \sin \varphi}{6} = \frac{\sqrt{\frac{5}{4}} \cdot \sqrt{\frac{5}{4}} \cdot 1 \cdot \sin 90^\circ}{6} = \frac{\frac{5}{4} \cdot 1}{6} = \frac{5}{4 \cdot 6} = \frac{5}{24}\). Ответ: \(\frac{5}{24}\) см³.
Дано: куб \(ABCDA_1B_1C_1D_1\) с ребром \(AA_1 = 1\) см. Точки \(E\) и \(F\) расположены на ребрах \(DC\) и \(BB_1\) соответственно так, что \(DE = EC\) и \(BF = FB_1\). Требуется найти объем тетраэдра \(AD_1EF\).
Решение начинается с обозначения длин ребер тетраэдра \(AF\) как \(a\) и \(D_1E\) как \(b\), а расстояние между ними \(AD\) как \(c\). Эти ребра лежат на скрещивающихся прямых, расположенных на противоположных гранях куба \(ABCDA_1B_1C_1D_1\).
Для нахождения угла между скрещивающимися прямыми \(AF\) и \(D_1E\), построим прямую, параллельную одной из них, проходящую через точку на другой прямой. Отметим точку \(F_1\) на ребре \(CC_1\) так, чтобы \(CF_1 = C_1F_1\). Поскольку \(BF = FB_1\), точка \(F\) является серединой ребра \(BB_1\). Аналогично, \(DE = EC\), так что \(E\) является серединой ребра \(DC\). Точка \(F_1\) является серединой ребра \(CC_1\). Рассмотрим вектор \(\vec{AF}\). Вектор \(\vec{D_1F_1}\) соединяет вершину \(D_1\) и середину ребра \(CC_1\). В кубе, если соединить середины двух противоположных ребер, полученный отрезок будет параллелен диагонали грани. В данном случае, \(AF\) соединяет вершину \(A\) с серединой \(F\) ребра \(BB_1\). \(D_1F_1\) соединяет вершину \(D_1\) с серединой \(F_1\) ребра \(CC_1\). Можно показать, что \(DF_1 \parallel AF\). Угол между скрещивающимися прямыми \(AF\) и \(D_1E\) равен углу между параллельной прямой \(DF_1\) и прямой \(D_1E\), то есть углу между прямыми \(DF_1\) и \(D_1E\). Точка \(M\) является точкой пересечения прямых \(D_1E\) и \(DF_1\). Угол между гранями тетраэдра \(AF\) и \(D_1E\) является \(\angle DMD_1 = \varphi\).
Рассмотрим прямоугольные треугольники \(\triangle ABF\) и \(\triangle DD_1E\). Они равны, так как \(AB = DD_1 = 1\) (ребро куба) и \(BF = DE = \frac{1}{2}\) (половины ребер). Длины ребер \(a\) и \(b\) можно найти по теореме Пифагора. Для \(a = AF\), рассмотрим прямоугольный треугольник \(ABF\). \(AF^2 = AB^2 + BF^2\). \(a = \sqrt{1^2 + (\frac{1}{2})^2} = \sqrt{1 + \frac{1}{4}} = \sqrt{\frac{5}{4}}\). Для \(b = D_1E\), рассмотрим прямоугольный треугольник \(DD_1E\). \(D_1E^2 = DD_1^2 + DE^2\). \(b = \sqrt{1^2 + (\frac{1}{2})^2} = \sqrt{1 + \frac{1}{4}} = \sqrt{\frac{5}{4}}\). Таким образом, \(a = b = \sqrt{\frac{5}{4}}\). Расстояние между гранями, на которых лежат ребра \(AF\) и \(D_1E\), равно ребру куба, то есть \(c = AD = 1\).
Рассмотрим также прямоугольные треугольники \(\triangle DD_1E\) и \(\triangle DCF_1\). Они равны, так как \(DD_1 = DC = 1\) и \(DE = CF_1 = \frac{1}{2}\). Следовательно, \(\angle CDF_1 = \angle DD_1E\).
Угол \(\angle D_1MD\) является углом между прямыми \(D_1E\) и \(DF_1\). В треугольнике \(D_1MD\), сумма углов равна \(180^\circ\). \(\angle MD_1D = 90^\circ\). Угол \(\angle D_1DM\) является частью угла \(\angle D_1DC = 90^\circ\). Угол \(\angle CDF_1 = \angle DD_1E\). В прямоугольном треугольнике \(DD_1E\), \(\tan(\angle DD_1E) = \frac{DE}{DD_1} = \frac{1/2}{1} = \frac{1}{2}\). В прямоугольном треугольнике \(DCF_1\), \(\tan(\angle DCF_1) = \frac{DF_1}{DC}\). Угол \(\angle D_1MD = 180^\circ — \angle MD_1D — \angle D_1DM = 180^\circ — 90^\circ — \angle D_1DM = \)
\(=90^\circ — \angle D_1DM\).
Угол \(\varphi = \angle D_1MD\). Из решения видно, что \(\varphi = 180^\circ — \angle CDF_1 — (90^\circ — \angle CDF_1) = 90^\circ\). Это означает, что прямые \(D_1E\) и \(DF_1\) перпендикулярны.
Объем тетраэдра, образованного скрещивающимися ребрами, может быть найден по формуле \(V = \frac{abc \cdot \sin \varphi}{6}\), где \(a\) и \(b\) — длины скрещивающихся ребер, \(c\) — расстояние между ними, и \(\varphi\) — угол между ними. Эта формула, как указано в задании, доказана в задаче 803.
Подставим найденные значения в формулу объема:
\(V_{тетр} = \frac{\sqrt{\frac{5}{4}} \cdot \sqrt{\frac{5}{4}} \cdot 1 \cdot \sin 90^\circ}{6}\).
Поскольку \(\sin 90^\circ = 1\), получаем:
\(V_{тетр} = \frac{\frac{5}{4} \cdot 1}{6} = \frac{\frac{5}{4}}{6} = \frac{5}{4 \cdot 6} = \frac{5}{24}\).
Таким образом, объем тетраэдра \(AD_1EF\) равен \(\frac{5}{24}\) см³.
Ответ: \(\frac{5}{24}\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!