ГДЗ по Геометрии 11 класс Номер 806 Атанасян — Подробные Ответы

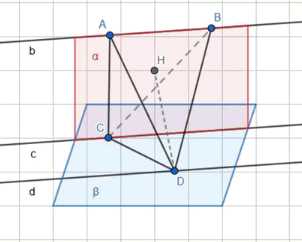
Даны три параллельные прямые, не лежащие в одной плоскости. На одной из них взят отрезок AB, а на двух других — точки С и D соответственно. Докажите, что объём тетраэдра ABCD не зависит от выбора точек С и D

Плоскость \(\alpha\) проходит через точки \(A\), \(B\), и \(C\). Поскольку точки \(A\) и \(B\) лежат на прямой \(b\), а точка \(C\) на прямой \(c\), и прямые \(b\) и \(c\) параллельны, плоскость \(\alpha\) определяется прямыми \(b\) и \(c\), и ее положение не зависит от конкретного выбора точки \(C\) на прямой \(c\). Прямая \(d\) параллельна прямым \(b\) и \(c\), следовательно, прямая \(d\) параллельна плоскости \(\alpha\). Высота \(DH\) от точки \(D\) до плоскости \(ABC\) (плоскости \(\alpha\)) является расстоянием между прямой \(d\) и плоскостью \(\alpha\). Поскольку \(d \parallel \alpha\), это расстояние постоянно для любой точки \(D\) на прямой \(d\), то есть \(DH\) не зависит от положения точки \(D\). Площадь треугольника \(ABC\), \(S_{ABC}\), может быть найдена как \(S_{ABC} = \frac{1}{2} \cdot AB \cdot h_C\), где \(h_C\) — высота, опущенная из точки \(C\) на прямую \(b\). Поскольку прямые \(b\) и \(c\) параллельны, расстояние между ними постоянно, и эта высота \(h_C\) не зависит от положения точки \(C\) на прямой \(c\). Таким образом, \(S_{ABC}\) не зависит от положения точки \(C\). Объем тетраэдра \(ABCD\) равен \(V_{ABCD} = \frac{1}{3} S_{ABC} \cdot DH\). Поскольку \(S_{ABC}\) не зависит от \(C\), а \(DH\) не зависит от \(D\), объем \(V_{ABCD}\) не зависит от положения точек \(C\) и \(D\). Что и требовалось доказать.

Дано, что прямые \(b\), \(c\), и \(d\) параллельны друг другу. Точки \(A\) и \(B\) лежат на прямой \(b\), точка \(C\) лежит на прямой \(c\), и точка \(D\) лежит на прямой \(d\). Необходимо доказать, что объем тетраэдра \(ABCD\), обозначаемый как \(V_{ABCD}\), не зависит от конкретного положения точек \(C\) и \(D\) на соответствующих прямых.

Для доказательства рассмотрим шаги.
Первый шаг заключается во введении плоскостей. Пусть плоскость \(\beta\) проходит через параллельные прямые \(c\) и \(d\). Пусть плоскость \(\alpha\) проходит через точки \(A\), \(B\) и \(C\).

Второй шаг анализирует плоскость \(\alpha\). Точки \(A\) и \(B\) принадлежат прямой \(b\). Точка \(C\) принадлежит прямой \(c\). Поскольку прямые \(b\) и \(c\) параллельны, плоскость \(\alpha\), содержащая прямую \(b\) (через точки \(A\) и \(B\)) и проходящая через точку \(C\) на прямой \(c\), однозначно определяется этими параллельными прямыми. Таким образом, положение плоскости \(\alpha\) не меняется при перемещении точки \(C\) вдоль прямой \(c\). Следовательно, плоскость \(\alpha\) не зависит от положения точки \(C\).

Третий шаг устанавливает отношение между прямой \(d\) и плоскостью \(\alpha\). Дано, что прямая \(d\) параллельна прямой \(b\), и прямая \(b\) параллельна прямой \(c\). Из свойства транзитивности параллельности прямых следует, что прямая \(d\) также параллельна прямой \(c\). Поскольку плоскость \(\alpha\) содержит прямую \(b\) и параллельна прямой \(c\) (так как \(b \parallel c\) и \(C \in c\)), и при этом прямая \(d\) параллельна как \(b\), так и \(c\), то прямая \(d\) должна быть параллельна плоскости \(\alpha\).

Четвертый шаг рассматривает высоту тетраэдра. Объем тетраэдра может быть вычислен по формуле \(V = \frac{1}{3} S_{основания} \cdot h_{высота}\). Рассмотрим треугольник \(ABC\) как основание тетраэдра \(ABCD\). Высота тетраэдра, опущенная из вершины \(D\) на плоскость основания \(ABC\), есть перпендикуляр \(DH\) к плоскости \(\alpha\), содержащей треугольник \(ABC\). Поскольку прямая \(d\), на которой лежит точка \(D\), параллельна плоскости \(\alpha\), расстояние от любой точки на прямой \(d\) до плоскости \(\alpha\) является постоянной величиной. Следовательно, длина высоты \(DH\) не зависит от конкретного положения точки \(D\) на прямой \(d\).

Пятый шаг анализирует площадь основания. Площадь треугольника \(ABC\), \(S_{ABC}\), может быть найдена как половина произведения длины стороны на высоту, опущенную на эту сторону. Возьмем сторону \(AB\). \(S_{ABC} = \frac{1}{2} \cdot AB \cdot h_{C, AB}\), где \(h_{C, AB}\) — высота, опущенная из точки \(C\) на прямую \(AB\). Поскольку точки \(A\) и \(B\) лежат на прямой \(b\), прямая \(AB\) совпадает с прямой \(b\). Таким образом, \(h_{C, AB}\) есть расстояние от точки \(C\) на прямой \(c\) до прямой \(b\). Так как прямые \(b\) и \(c\) параллельны, расстояние между ними постоянно. Следовательно, высота \(h_{C, AB}\) не зависит от положения точки \(C\) на прямой \(c\). Длина отрезка \(AB\) фиксирована, так как \(A\) и \(B\) — заданные точки на прямой \(b\). Поэтому площадь основания \(S_{ABC}\) не зависит от положения точки \(C\).

Наконец, объединяя результаты, объем тетраэдра \(V_{ABCD}\) дается формулой \(V_{ABCD} = \frac{1}{3} S_{ABC} \cdot DH\). Мы показали, что площадь основания \(S_{ABC}\) не зависит от положения точки \(C\), а высота \(DH\) не зависит от положения точки \(D\). Следовательно, произведение \(S_{ABC} \cdot DH\) является постоянной величиной, и объем \(V_{ABCD}\) не зависит от положения точек \(C\) и \(D\). Это завершает доказательство.