
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 805 Атанасян — Подробные Ответы
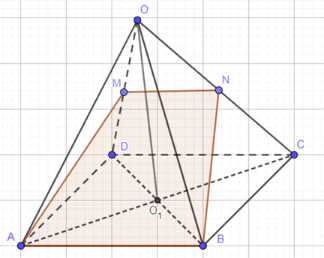
Основанием пирамиды OABCD является параллелограмм ABCD. В каком отношении делит объём пирамиды плоскость, проходящая через прямую АВ и среднюю линию грани OCD?
Опустим перпендикуляры на \(ABCD\): \(OO_1 \perp ABCD\), \(NN_1 \perp ABCD\), \(V_{OABCD} = V\). \(S_{ABC} = \frac{1}{2}S_{ABCD}\), \(NN_1 = \frac{1}{2}OO_1\), \(V_{ABCN} = \frac{1}{4}V\). \(ON = CN\), \(S_{BNO} = S_{BCN}\), \(V_{ABNO} = V_{ABCN} = \frac{1}{4}V\). \(S_{ACD} = \frac{1}{2}S_{ABCD}\), \(V_{AOCD} = \frac{1}{2}V_{OABCD} = \frac{1}{2}V\). \(MN\) — средняя линия в \(\triangle OCD\): \(S_{OMN} = \frac{1}{4}S_{OCD}\), \(V_{AOMN} = \frac{1}{4}V_{AOCD} = \frac{1}{8}V\). Найдем отношение объемов тел: \(V_{ABMNO} = V_{AOMN} + V_{ABNO} = \frac{1}{8}V + \frac{1}{4}V = \frac{3}{8}V\). \(V_{ABCDMN} = V — V_{ABMNO} = V — \frac{3}{8}V = \frac{5}{8}V\). \(V_{ABMNO} : V_{ABCDMN} = \frac{3}{8} : \frac{5}{8} = 3 : 5\).
Опустим перпендикуляры из вершин \(O\) и \(N\) на плоскость основания \(ABCD\). Пусть \(OO_1\) и \(NN_1\) будут эти перпендикуляры. \(OO_1\) является высотой пирамиды \(OABCD\), и мы обозначим объем этой пирамиды как \(V\), так что \(V = \frac{1}{3} \cdot S_{ABCD} \cdot OO_1\).
Площадь треугольника \(ABC\) составляет половину площади основания \(ABCD\), то есть \(S_{ABC} = \frac{1}{2}S_{ABCD}\). Поскольку \(N\) является серединой ребра \(OC\), а \(NN_1\) и \(OO_1\) перпендикулярны одной и той же плоскости \(ABCD\), отрезок \(NN_1\) параллелен \(OO_1\). Из подобия треугольников следует, что длина \(NN_1\) равна половине длины \(OO_1\), то есть \(NN_1 = \frac{1}{2}OO_1\). Объем пирамиды \(ABCN\) (с основанием \(ABC\) и вершиной \(N\)) равен \(V_{ABCN} = \frac{1}{3} \cdot S_{ABC} \cdot NN_1\). Подставляя выражения для \(S_{ABC}\) и \(NN_1\), получаем \(V_{ABCN} = \frac{1}{3} \cdot (\frac{1}{2}S_{ABCD}) \cdot (\frac{1}{2}OO_1) = \frac{1}{4} \cdot (\frac{1}{3} S_{ABCD} \cdot OO_1)\). Поскольку \(V = \frac{1}{3} S_{ABCD} \cdot OO_1\), имеем \(V_{ABCN} = \frac{1}{4}V\).
Дано, что \(N\) является серединой ребра \(OC\), то есть \(ON = CN\). В треугольнике \(BOC\), отрезок \(BN\) является медианой, которая делит треугольник на два равновеликих треугольника, поэтому \(S_{\triangle BNO} = S_{\triangle BCN}\). Рассмотрим пирамиды с общей вершиной \(A\) и основаниями \(\triangle BNO\) и \(\triangle BCN\). Эти пирамиды имеют общую высоту, опущенную из вершины \(A\) на плоскость \(OBC\). Объемы таких пирамид относятся как площади их оснований. Поскольку \(S_{\triangle BNO} = S_{\triangle BCN}\), объемы пирамид \(A-BNO\) и \(A-BCN\) равны: \(V_{A-BNO} = V_{A-BCN}\). В соответствии с обозначениями в условии задачи, примем, что \(V_{ABNO} = V_{ABCN}\). Из предыдущего шага мы знаем, что \(V_{ABCN} = \frac{1}{4}V\), следовательно, \(V_{ABNO} = \frac{1}{4}V\).
Площадь треугольника \(ACD\) составляет половину площади основания \(ABCD\), то есть \(S_{AC
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!