Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 804 Атанасян — Подробные Ответы
Докажите, что плоскость, проходящая через ребро и середину противоположного ребра тетраэдра, разделяет его на две части, объёмы которых равны.
Опустим перпендикуляры на плоскость \(ABC\). \(DH \perp ABC\), \(MH_1 \perp ABC\), следовательно \(DH \parallel MH_1\).
Рассмотрим треугольник \(DHB\). Так как \(DM = MB\) и \(MH_1 \parallel DH\), \(MH_1\) является средней линией треугольника \(DHB\).
Следовательно, \(MH_1 = \frac{1}{2} DH\).
Объем тетраэдра \(VACBD\) равен \(V_{ACBD} = \frac{1}{3} S_{ABC} \cdot DH\).
Объем тетраэдра \(VACBM\) равен \(V_{ACBM} = \frac{1}{3} S_{ABC} \cdot MH_1\).
Подставим выражение для \(MH_1\) в формулу для \(V_{ACBM}\): \(V_{ACBM} = \frac{1}{3} S_{ABC} \cdot \frac{1}{2} DH = \frac{1}{2} \left( \frac{1}{3} S_{ABC} \cdot DH \right) = \frac{1}{2} V_{ACBD}\).
Таким образом, \(V_{ACBM} = \frac{1}{2} V_{ACBD}\).
Тетраэдры \(V_{ACBM}\) и \(V_{ACMD}\) имеют общую грань \(ACM\). Сумма их объемов равна объему тетраэдра \(V_{ACBD}\).
\(V_{ACBM} + V_{ACMD} = V_{ACBD}\).
Подставим \(V_{ACBM} = \frac{1}{2} V_{ACBD}\): \(\frac{1}{2} V_{ACBD} + V_{ACMD} = V_{ACBD}\).
Отсюда \(V_{ACMD} = V_{ACBD} — \frac{1}{2} V_{ACBD} = \frac{1}{2} V_{ACBD}\).
Следовательно, \(V_{ACBM} = V_{ACMD}\).
Что и требовалось доказать.
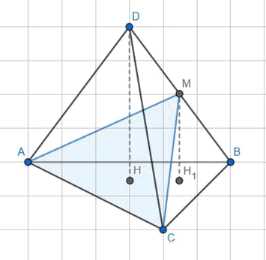
Дан тетраэдр ABCD, сечение AMC, и известно, что \(DM = MB\). Необходимо доказать, что объемы тетраэдров ABCM и ACMD равны, то есть \(V_{ABCM} = V_{ACMD}\).
Доказательство состоит из следующих шагов.
1) Опустим перпендикуляры из вершин D и M на плоскость основания ABC. Пусть \(DH \perp ABC\) и \(MH_1 \perp ABC\). Поскольку обе прямые DH и MH1 перпендикулярны одной и той же плоскости ABC, они параллельны друг другу, то есть \(DH \parallel MH_1\).
2) Рассмотрим треугольник DHB. Из условия дано, что \(DM = MB\). Поскольку \(DH \perp ABC\) и \(MH_1 \perp ABC\), то \(DH \perp HB\) и \(MH_1 \perp HB_1\) (где \(H_1\) лежит на HB). Так как \(DH \parallel MH_1\), и M является серединой DB, а \(MH_1 \parallel DH\), то \(MH_1\) является средней линией треугольника DHB, проведенной из середины стороны DB к стороне HB. Следовательно, \(MH_1 = \frac{1}{2}DH\).
3) Объем тетраэдра вычисляется по формуле \(V = \frac{1}{3} \cdot S_{осн} \cdot h\), где \(S_{осн}\) — площадь основания, а \(h\) — высота.
Объем тетраэдра ACBD (или ABCD) с основанием ABC и высотой DH равен \(V_{ACBD} = \frac{1}{3} \cdot S_{ABC} \cdot DH\).
Объем тетраэдра ABCM с основанием ABC и высотой \(MH_1\) равен \(V_{ABCM} = \frac{1}{3} \cdot S_{ABC} \cdot MH_1\).
Используя соотношение \(MH_1 = \frac{1}{2}DH\), полученное на шаге 2, подставим его в формулу для объема \(V_{ABCM}\):
\(V_{ABCM} = \frac{1}{3} \cdot S_{ABC} \cdot (\frac{1}{2}DH) = \frac{1}{2} \cdot (\frac{1}{3} \cdot S_{ABC} \cdot DH)\).
Таким образом, \(V_{ABCM} = \frac{1}{2}V_{ACBD}\).
Теперь рассмотрим тетраэдры ABCM и ACMD. Они имеют общую грань AMC.
Объем тетраэдра ABCM можно также рассматривать как объем с основанием AMC и высотой, опущенной из B на плоскость AMC.
Объем тетраэдра ACMD можно рассматривать как объем с основанием AMC и высотой, опущенной из D на плоскость AMC.
Однако, более простой способ заключается в сравнении объемов \(V_{ABCM}\) и \(V_{ACMD}\) через их отношение к объему всего тетраэдра \(V_{ACBD}\).
Мы уже показали, что \(V_{ABCM} = \frac{1}{2}V_{ACBD}\).
Рассмотрим тетраэдр ACMD. Его объем \(V_{ACMD}\) также связан с объемом \(V_{ACBD}\).
Поскольку M является серединой ребра DB, тетраэдры ACMD и ABCM имеют общую грань AMC и вершины D и B расположены по разные стороны от плоскости AMC. Расстояния от D и B до плоскости AMC пропорциональны расстояниям от D и B до плоскости, проходящей через AC и параллельной DB.
Так как M — середина DB, то расстояние от D до плоскости AMC равно расстоянию от B до плоскости AMC.
Следовательно, высоты тетраэдров ACMD и ABCM, опущенные из вершин D и B на общую грань AMC, равны.
Поскольку у тетраэдров ABCM и ACMD общая грань AMC и равные высоты, опущенные на эту грань, их объемы равны: \(V_{ABCM} = V_{ACMD}\).
Также можно рассмотреть, что тетраэдры ABCM и ACMD составляют весь тетраэдр ACBD, то есть \(V_{ACBD} = V_{ABCM} + V_{ACMD}\).
Так как \(V_{ABCM} = \frac{1}{2}V_{ACBD}\), подставим это в предыдущее равенство:
\(V_{ACBD} = \frac{1}{2}V_{ACBD} + V_{ACMD}\).
Отсюда следует, что \(V_{ACMD} = V_{ACBD} — \frac{1}{2}V_{ACBD} = \frac{1}{2}V_{ACBD}\).
Таким образом, \(V_{ABCM} = \frac{1}{2}V_{ACBD}\) и \(V_{ACMD} = \frac{1}{2}V_{ACBD}\), откуда следует, что \(V_{ABCM} = V_{ACMD}\).
Что и требовалось доказать.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.