Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 803 Атанасян — Подробные Ответы
Докажите, что объём тетраэдра равен \(\frac{1}{6}abc \sin \phi\), где а и b — противоположные рёбра, а \(\phi\) и с — соответственно угол и расстояние между ними.
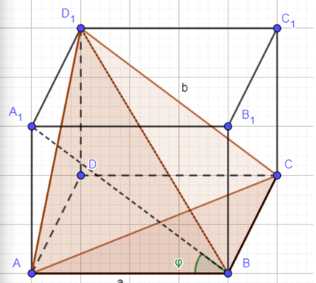
Достроим тетраэдр до параллелепипеда. Угол между прямыми \(AB\) и \(CD_1\) равен углу \(\angle A_1BA\), то есть \(\angle A_1BA = \phi\). Расстояние между прямыми \(AB\) и \(CD_1\) равно высоте параллелепипеда, опущенной на плоскость грани \(AA_1BB_1\), что равно \(AD = c\). Площадь грани \(AA_1BB_1\) равна \(S_{AA_1BB_1} = AB \cdot BA_1 \sin \angle ABA_1 = a \cdot b \sin \phi\). Объем параллелепипеда равен произведению площади основания на высоту, то есть \(V_{парал} = S_{AA_1BB_1} \cdot AD = ab \sin \phi \cdot c = abc \sin \phi\). Объем данного тетраэдра составляет \(\frac{1}{6}\) объема построенного параллелепипеда, то есть \(V_{тетр} = \frac{1}{6} V_{парал} = \frac{1}{6} abc \sin \phi\).
Для решения данной задачи достроим данный тетраэдр \(ABCD_1\) до параллелепипеда \(AA_1BB_1D_1C_1CD\). Это можно сделать, построив плоскости, проходящие через ребра тетраэдра параллельно противоположным ребрам. Например, через ребро \(AB\) проведем плоскость, параллельную \(CD_1\), и через ребро \(CD_1\) проведем плоскость, параллельную \(AB\). Аналогично поступим с другими парами скрещивающихся ребер. В результате получим параллелепипед, в котором ребра \(AB\) и \(CD_1\) являются скрещивающимися диагоналями смежных граней или ребрами.
В построенном параллелепипеде \(AA_1BB_1D_1C_1CD\) ребро \(AB\) параллельно ребру \(CD_1C\) и равно ему по длине, а ребро \(CD_1\) параллельно ребру \(ABB_1\) и равно ему по длине. По условию дано, что длина ребра \(AB = a\) и длина ребра \(CD_1 = b\). Угол между скрещивающимися прямыми \(AB\) и \(CD_1\) по условию равен \(\phi\). Этот угол равен углу между прямой \(AB\) и любой прямой, параллельной \(CD_1\) и пересекающей \(AB\). В нашем построенном параллелепипеде прямая \(A_1B\) параллельна \(CD_1\). Следовательно, угол между прямыми \(AB\) и \(CD_1\) равен углу между прямыми \(AB\) и \(A_1B\), то есть \(\angle A_1BA = \phi\).
Расстояние между скрещивающимися прямыми \(AB\) и \(CD_1\) по условию равно \(c\). В построенном параллелепипеде это расстояние равно расстоянию между параллельными плоскостями, содержащими эти прямые. Одной из таких плоскостей является плоскость грани \(AA_1BB_1\), содержащая прямую \(AB\). Другой плоскостью является плоскость, проходящая через \(CD_1\) параллельно \(AA_1BB_1\). Расстояние между этими плоскостями равно высоте параллелепипеда, опущенной из любой точки одной плоскости на другую. В данном случае это расстояние равно длине ребра \(AD\), перпендикулярного плоскости \(AA_1BB_1\). Таким образом, \(AD = c\).
Теперь найдем объем построенного параллелепипеда. Объем параллелепипеда равен произведению площади основания на высоту. В качестве основания выберем грань \(AA_1BB_1\). Эта грань является параллелограммом со сторонами \(AB\) и \(A_1B\). Длина стороны \(AB = a\), а длина стороны \(A_1B = b\) (так как \(A_1B\) параллельна и равна \(CD_1\)). Угол между сторонами \(AB\) и \(A_1B\) равен \(\angle A_1BA = \phi\). Площадь параллелограмма \(AA_1BB_1\) вычисляется по формуле: \(S_{AA_1BB_1} = AB \cdot A_1B \sin \angle A_1BA = a \cdot b \sin \phi\).
Высота параллелепипеда, соответствующая основанию \(AA_1BB_1\), равна расстоянию между плоскостью \(AA_1BB_1\) и противоположной плоскостью \(DD_1C_1C\). Это расстояние равно длине ребра \(AD = c\).
Таким образом, объем параллелепипеда \(V_{парал}\) равен произведению площади основания \(S_{AA_1BB_1}\) на высоту \(AD\): \(V_{парал} = S_{AA_1BB_1} \cdot AD = (ab \sin \phi) \cdot c = abc \sin \phi\).
Существует теорема, согласно которой объем тетраэдра, являющегося частью параллелепипеда и имеющего с ним общую вершину, а три ребра, выходящие из этой вершины, совпадают с ребрами параллелепипеда, равен \(\frac{1}{6}\) объема этого параллелепипеда. В нашем случае тетраэдр \(ABCD_1\) не имеет общей вершины с построенным параллелепипедом в таком виде, чтобы его ребра совпадали с ребрами параллелепипеда. Однако, объем любого тетраэдра, вписанного в параллелепипед таким образом, что его вершины совпадают с вершинами параллелепипеда, составляет \(\frac{1}{6}\) объема этого параллелепипеда. Данный тетраэдр \(ABCD_1\) является таким тетраэдром.
Следовательно, объем тетраэдра \(V_{тетр}\) равен \(\frac{1}{6}\) объема построенного параллелепипеда \(V_{парал}\): \(V_{тетр} = \frac{1}{6} V_{парал} = \frac{1}{6} abc \sin \phi\).
Полученный результат \(V_{тетр} = \frac{1}{6} abc \sin \phi\) совпадает с выражением, которое требовалось доказать.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.