
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 802 Атанасян — Подробные Ответы
Плоскости AB1C1 и А ВС разбивают треугольную призму ABCA1B1C1 на четыре части. Найдите отношение объёмов этих частей.
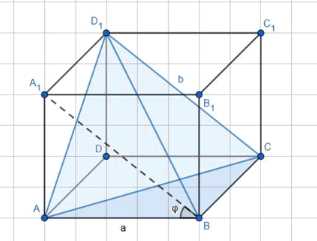
Достроим тетраэдр до параллелепипеда, построенного на ребрах, параллельных \(AB\), \(CD_1\) и перпендикулярных им. Длины этих ребер равны \(a\), \(b\), и \(c\) соответственно. Угол между ребрами длиной \(a\) и \(b\) равен \(\phi\). Площадь грани параллелепипеда, образованной векторами, параллельными \(AB\) и \(CD_1\), равна \(ab \sin \phi\). Высота параллелепипеда, опущенная на эту грань, равна расстоянию между \(AB\) и \(CD_1\), то есть \(c\). Объем параллелепипеда равен произведению площади основания на высоту, что составляет \(V_{\text{парал}} = (ab \sin \phi) \cdot c = abc \sin \phi\). Объем данного тетраэдра составляет \(\frac{1}{6}\) объема этого параллелепипеда. Следовательно, \(V_{\text{тетр}} = \frac{1}{6} V_{\text{парал}} = \frac{1}{6} abc \sin \phi\). Что и требовалось доказать.
Для начала, представим, что данный тетраэдр можно достроить до параллелепипеда. Этот параллелепипед построен на трех ребрах, которые параллельны \(AB\), \(CD_1\) и перпендикулярны им. Длины этих ребер обозначим как \(a\), \(b\), и \(c\) соответственно. Пусть угол между ребрами длиной \(a\) и \(b\) равен \(\phi\). Площадь грани этого параллелепипеда, которая образована векторами, параллельными \(AB\) и \(CD_1\), может быть найдена как произведение длин этих векторов на синус угла между ними, то есть \(ab \sin \phi\). Высота параллелепипеда, опущенная на эту грань, равна расстоянию между прямыми \(AB\) и \(CD_1\), которое по условию равно \(c\). Объем параллелепипеда равен произведению площади основания на высоту. Таким образом, объем параллелепипеда составляет \(V_{\text{парал}} = (ab \sin \phi) \cdot c = abc \sin \phi\). Известно, что объем тетраэдра, построенного на трех некомпланарных векторах, исходящих из одной вершины, составляет одну шестую объема параллелепипеда, построенного на этих же векторах. В данном случае, объем тетраэдра составляет \(\frac{1}{6}\) объема построенного параллелепипеда. Следовательно, объем тетраэдра равен \(V_{\text{тетр}} = \frac{1}{6} V_{\text{парал}} = \frac{1}{6} abc \sin \phi\). Таким образом, мы получили формулу для объема тетраэдра, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!