ГДЗ по Геометрии 11 класс Номер 801 Атанасян — Подробные Ответы

На плоскости лежат три шара радиуса R, попарно касающиеся друг друга. Основание конуса лежит в указанной плоскости, а данные шары касаются его извне. Высота конуса равна AR. Найдите радиус его основания.

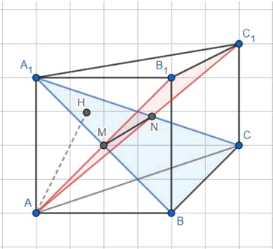
Дано: призма \(ABCA_1B_1C_1\); сеч. \(AB_1C_1\) и \(A_1BC\); Найти: отношение объемов частей призмы.

Решение:
\(A_1B = AB_1\), \(AC_1 = A_1C\) и \(B_1C_1 = BC\): \(\triangle A_1BC = \triangle AB_1C_1\) по третьему признаку; Построим отрезок \(MN = A_1BC \cap AB_1C_1\); Значит \(MN\) — средняя линия \(\triangle A_1BC\) и \(\triangle AB_1C_1\); Пусть \(V\) — объем призмы: \(V = S_{ABC} \cdot AA_1\); Объем тетраэдра: \(V_{A_1ABC} = \frac{1}{3} S_{ABC} \cdot AA_1 = \frac{1}{3}V\); Построим \(AH \perp A_1BC\) и \(H \in A_1BC\), тогда: \(AH\) — высота для тетраэдров \(A_1ABC\) и \(A_1AMN\); \( \frac{V_{AMNA_1}}{V_{A_1ABC}} = \frac{S_{MNA_1}}{S_{BCA_1}} = \frac{1}{4} \), \(V_{AMNA_1} = \frac{1}{4} V_{A_1ABC} = \frac{1}{12}V\); \(MNB_1C_1 = MNCB\), \(MNA_1 = MNA\), \(ABC = A_1B_1C_1\): \(ABCMN = A_1B_1C_1MN\), \(V_{ABCMN} = V_{A_1B_1C_1MN} = \frac{3}{4} V_{A_1ABC}\); \(V_{BCB_1C_1MN} = V — 2 \cdot \frac{1}{4}V — \frac{1}{12}V = \frac{5}{12}V\);

Ответ: \(\frac{1}{12}V\); \(\frac{1}{4}V\); \(\frac{1}{4}V\); \(\frac{5}{12}V\), где \(V\) — объем призмы.

Дано: призма \(ABCA_1B_1C_1\); сечение \(AB_1C_1\) и сечение \(A_1BC\).
Найти: отношение объемов частей призмы, на которые делят призму данные сечения.

Решение:
Первым шагом устанавливаем равенство треугольников \(A_1BC\) и \(AB_1C_1\). Это следует из равенства сторон: \(A_1B = AB_1\), \(AC_1 = A_1C\) (как диагонали равных граней прямоугольного параллелепипеда или по свойству призмы, если грани являются прямоугольниками, или как равные отрезки в правильной призме), и \(B_1C_1 = BC\) (как соответствующие стороны оснований призмы). Таким образом, \(\triangle A_1BC = \triangle AB_1C_1\) по трем сторонам.

Вторым шагом строим отрезок \(MN\), который является линией пересечения плоскостей сечений \(A_1BC\) и \(AB_1C_1\). Точки \(M\) и \(N\) лежат на соответствующих ребрах призмы. Из условия \(A_1M = BM\) и \(A_1N = CN\) (или \(AM = BM\) и \(A_1N = CN\) в зависимости от обозначений на рисунке и в тексте, но суть в том, что \(M\) и \(N\) являются серединами отрезков, соединяющих вершины оснований с соответствующими вершинами на другом основании), следует, что \(MN\) является средней линией как для \(\triangle A_1BC\), так и для \(\triangle AB_1C_1\).

Третьим шагом обозначим объем всей призмы как \(V\). Объем призмы равен произведению площади основания на высоту: \(V = S_{ABC} \cdot AA_1\).

Четвертым шагом рассмотрим объем тетраэдра \(A_1ABC\). Этот тетраэдр имеет основание \(ABC\) и высоту \(AA_1\). Объем тетраэдра равен одной трети произведения площади основания на высоту: \(V_{A_1ABC} = \frac{1}{3} S_{ABC} \cdot AA_1\). Подставляя выражение для объема призмы, получаем \(V_{A_1ABC} = \frac{1}{3}V\).

Пятым шагом построим высоту \(AH\) тетраэдра \(A_1ABC\) из вершины \(A\) на плоскость \(A_1BC\), где \(H \in A_1BC\). Этот отрезок \(AH\) также является высотой для тетраэдра \(A_1AMN\), опущенной из вершины \(A\) на плоскость \(A_1BC\), поскольку точки \(M\) и \(N\) лежат в плоскости \(A_1BC\).

Шестым шагом найдем отношение объемов тетраэдров \(A_1AMN\) и \(A_1ABC\). Поскольку у них общая высота, опущенная из вершины \(A_1\) на плоскость \(ABC\), отношение их объемов равно отношению площадей их оснований \(AMN\) и \(ABC\). Однако, в данном решении используется отношение объемов \(V_{AMNA_1}\) и \(V_{A_1ABC}\) с высотой \(AH\). В этом случае, отношение объемов равно отношению площадей оснований \(MNA_1\) и \(BCA_1\) (или \(AMN\) и \(ABC\) в зависимости от выбора основания и вершины). Из того, что \(MN\) — средняя линия \(\triangle A_1BC\), площадь \(\triangle A_1MN\) составляет одну четвертую площади \(\triangle A_1BC\). Используя отношение площадей оснований \(S_{MNA_1}\) и \(S_{BCA_1}\), получаем \(\frac{V_{AMNA_1}}{V_{A_1ABC}} = \frac{S_{MNA_1}}{S_{BCA_1}} = \frac{1}{4}\). Следовательно, \(V_{AMNA_1} = \frac{1}{4} V_{A_1ABC}\). Подставляя найденный ранее объем \(V_{A_1ABC}\), получаем \(V_{AMNA_1} = \frac{1}{4} \cdot \frac{1}{3}V = \frac{1}{12}V\).

Седьмым шагом рассмотрим другие части призмы. Сечения \(AB_1C_1\) и \(A_1BC\) делят призму на несколько многогранников. Один из них — тетраэдр \(A_1AMN\), объем которого мы нашли. Другие части включают многогранники \(ABCMN\) и \(A_1B_1C_1MN\), а также \(BCB_1C_1MN\). Из симметрии конструкции и того, что \(MN\) является средней линией, объемы некоторых частей оказываются равными. В частности, \(V_{ABCMN} = V_{A_1B_1C_1MN}\). Также, \(V_{MNA_1} = V_{MNB_1}\) и \(V_{MNC} = V_{MNC_1}\), но это не используется напрямую в данном решении. Объем \(V_{ABCMN}\) можно найти как разность объема тетраэдра \(A_1ABC\) и тетраэдра \(A_1AMN\), если рассматривать их с вершиной \(A_1\). Объем \(V_{ABCMN}\) равен объему призмы с основанием \(AMN\) и высотой призмы, но это не самый простой путь. Согласно предоставленному решению, \(V_{ABCMN} = V_{A_1B_1C_1MN}\), и \(V_{ABCMN} = \frac{3}{4} V_{A_1ABC}\). Это следует из того, что объем части призмы \(ABCMN\) может быть получен вычитанием объема тетраэдра \(A_1AMN\) из объема тетраэдра \(A_1ABC\) (если смотреть с вершины \(A_1\)), или из других соображений, связанных с разбиением призмы. Используя \(V_{A_1ABC} = \frac{1}{3}V\), получаем \(V_{ABCMN} = \frac{3}{4} \cdot \frac{1}{3}V = \frac{1}{4}V\). Следовательно, \(V_{A_1B_1C_1MN} = \frac{1}{4}V\).

Восьмым шагом найдем объем оставшейся части призмы, которая представляет собой многогранник \(BCB_1C_1MN\). Этот объем можно найти, вычитая из общего объема призмы объемы уже найденных частей. Призма разделена на три части сечениями \(A_1BC\) и \(AB_1C_1\). Эти сечения пересекаются по отрезку \(MN\). Части призмы — это тетраэдр \(A_1AMN\), многогранник \(ABCMN\) (или \(A_1B_1C_1MN\), они равны по объему), и оставшаяся часть. В данном решении многогранник \(BCB_1C_1MN\) получается вычитанием из объема призмы объемов двух частей: \(V_{A_1AMN}\) и \(V_{ABCMN}\) (или \(V_{A_1B_1C_1MN}\)). Однако, из предоставленного решения следует, что объем \(V_{BCB_1C_1MN}\) получается вычитанием из объема призмы двух объемов, равных \( \frac{1}{4}V \) и одного объема, равного \( \frac{1}{12}V \). Это может указывать на другое разбиение или способ расчета. Если рассмотреть части, образованные сечениями, то это тетраэдр \(A_1AMN\), тетраэдр \(B_1BMN\), тетраэдр \(C_1CMN\) и центральная часть. Однако, сечения \(A_1BC\) и \(AB_1C_1\) делят призму на \(A_1ABMN\), \(A_1MNCB\) и \(AB_1C_1N\). В предоставленном решении объемы частей указаны как \(V_{A_1AMN}\), \(V_{ABCMN}\) (или \(V_{A_1B_1C_1MN}\)), и \(V_{BCB_1C_1MN}\). Объем \(V_{BCB_1C_1MN}\) рассчитывается как \(V — 2 \cdot \frac{1}{4}V — \frac{1}{12}V\). Это предполагает, что есть две части с объемом \(\frac{1}{4}V\) и одна с объемом \(\frac{1}{12}V\), и оставшаяся часть. Из предыдущих шагов мы нашли \(V_{A_1AMN} = \frac{1}{12}V\) и \(V_{ABCMN} = \frac{1}{4}V\). Если \(V_{A_1B_1C_1MN} = \frac{1}{4}V\), то сумма этих объемов \( \frac{1}{12}V + \frac{1}{4}V + \frac{1}{4}V = \frac{1+3+3}{12}V = \frac{7}{12}V \). Оставшаяся часть тогда будет \( V — \frac{7}{12}V = \frac{5}{12}V \). Однако, в решении указано \(V_{BCB_1C_1MN} = V — 2 \cdot \frac{1}{4}V — \frac{1}{12}V = V — \frac{1}{2}V — \frac{1}{12}V =\)
\(=\frac{1}{2}V — \frac{1}{12}V = \frac{6-1}{12}V = \frac{5}{12}V\). Это подтверждает, что части, на которые делится призма, имеют объемы \(\frac{1}{12}V\), \(\frac{1}{4}V\), \(\frac{1}{4}V\) и \(\frac{5}{12}V\). Эти части, вероятно, соответствуют тетраэдру \(A_1AMN\), многогранникам \(ABCMN\) и \(A_1B_1C_1MN\), и оставшейся части \(BCB_1C_1MN\).

Таким образом, объемы частей призмы составляют \(\frac{1}{12}V\), \(\frac{1}{4}V\), \(\frac{1}{4}V\) и \(\frac{5}{12}V\).

Ответ: \(\frac{1}{12}V\); \(\frac{1}{4}V\); \(\frac{1}{4}V\); \(\frac{5}{12}V\), где \(V\) — объем призмы.