Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 800 Атанасян — Подробные Ответы
На плоскости лежат четыре шара радиуса R, причём три из них попарно касаются друг друга, а четвёртый касается двух из них. На эти шары положены сверху два шара меньшего радиуса r, касающиеся друг друга, причём каждый из них касается трёх больших шаров. Найдите радиус маленьких шаров.
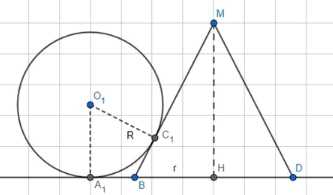
Рассмотрим один шар радиуса \(R\) с центром \(O_1\), касающийся плоскости в точке \(A_1\) и конуса в точке \(C_1\). Осевое сечение конуса \(MBD\) имеет \(BH = HD = r\). Четырехугольник \(A_1BC_1O_1\) имеет прямые углы при \(A_1\) и \(C_1\), и \(A_1B = C_1B\). Угол \(A_1O_1C_1 = 180^\circ — \angle A_1BC_1 = \angle C_1BH\), и \( \angle A_1O_1B = \frac{1}{2} \angle C_1BH \). В прямоугольном треугольнике \(MBH\), \( \text{tg} \angle MBH = \frac{MH}{BH} = \frac{\lambda R}{r} \). Точка \(H\) является центром основания конуса и центром треугольника \(A_1A_2A_3\), образованного точками касания шаров с плоскостью. \( A_1H = \frac{A_1A_2}{\sqrt{3}} = \frac{2\sqrt{3}R}{3} \). \( A_1B = A_1H — BH = \frac{2\sqrt{3}R}{3} — r \). Используя формулу тангенса половинного угла, \( \text{tg} \frac{\angle MBH}{2} = \frac{A_1B}{R} = \frac{\frac{2\sqrt{3}}{3}R — r}{R} \). Подставляя это в формулу \( \text{tg} \angle MBH = \frac{2 \text{tg} \frac{\angle MBH}{2}}{1 — \text{tg}^2 \frac{\angle MBH}{2}} \) и приравнивая к \( \frac{\lambda R}{r} \), получаем уравнение \( \frac{\lambda R}{r} = \frac{2(\frac{2\sqrt{3}}{3} — \frac{r}{R})}{1 — (\frac{2\sqrt{3}}{3} — \frac{r}{R})^2} \). После упрощения данного выражения приходим к квадратному уравнению относительно \(r\): \( 3(\lambda — 2)r^2 — 4\sqrt{3}R(\lambda — 1)r + \lambda R^2 = 0 \).
Если \( \lambda = 2 \), уравнение сводится к \( -4\sqrt{3}R(1)r + 2R^2 = 0 \), откуда \( r = \frac{2R^2}{4\sqrt{3}R} = \frac{R}{2\sqrt{3}} = \frac{R\sqrt{3}}{6} \).
Если \( \lambda \neq 2 \), решаем квадратное уравнение и получаем \( r = R \cdot \frac{2\sqrt{3}(\lambda — 1) — \sqrt{9\lambda^2 — 18\lambda + 12}}{3(\lambda — 2)} \).
Ответ: \( r = R \cdot \frac{2\sqrt{3}(\lambda — 1) — \sqrt{9\lambda^2 — 18\lambda + 12}}{3(\lambda — 2)} \) при \( \lambda \neq 2 \); \( r = \frac{R\sqrt{3}}{6} \) при \( \lambda = 2 \).
Дано: три шара радиуса \(R\) лежат на плоскости и попарно касаются друг друга. Конус имеет основание с центром \(H\) и радиусом \(r\) на той же плоскости. Все шары касаются конуса извне. Высота конуса \(h = \lambda R\). Необходимо найти радиус основания конуса \(r\).
Решение:
Поскольку все шары имеют одинаковый радиус и попарно касаются друг друга, их центры \(O_1\), \(O_2\), \(O_3\) образуют равносторонний треугольник со стороной \(2R\). Точки касания этих шаров с плоскостью \(a\), обозначим их \(A_1\), \(A_2\), \(A_3\), также образуют равносторонний треугольник со стороной \(2R\). Центр \(H\) основания конуса совпадает с центром этого треугольника \(A_1A_2A_3\).
Рассмотрим один шар с центром \(O_1\) и радиусом \(R\). Точка \(A_1\) — это точка касания шара с плоскостью \(a\). Точка \(C_1\) — это точка касания шара с конусом.
Осевое сечение конуса — треугольник \(MBD\), где \(M\) — вершина конуса, \(BD\) — диаметр основания, проходящий через \(H\). \(BH = HD = r\). Высота конуса \(MH = h = \lambda R\).
Рассмотрим четырехугольник \(A_1BC_1O_1\), где \(B\) — точка на основании конуса, лежащая на отрезке \(A_1H\). Углы \( \angle O_1A_1B \) и \( \angle O_1C_1B \) прямые, поскольку \(O_1A_1\) перпендикулярно плоскости \(a\) и \(O_1C_1\) перпендикулярно касательной плоскости к конусу в точке \(C_1\). Треугольники \( \Delta O_1A_1B \) и \( \Delta O_1C_1B \) равны по гипотенузе (\(O_1B\)) и катету (\(O_1A_1 = O_1C_1 = R\)). Следовательно, \(A_1B = C_1B\). Угол \( \angle A_1O_1C_1 = 180^\circ — \angle A_1BC_1 \). Угол \( \angle A_1BC_1 \) является внешним углом для треугольника \(C_1BH\). Угол \( \angle C_1BH \) — это угол между образующей конуса \(MB\) и плоскостью основания, который совпадает с углом \( \angle MBH \). Таким образом, \( \angle A_1O_1C_1 = \angle C_1BH = \angle MBH \). Из равенства треугольников \( \Delta O_1A_1B \) и \( \Delta O_1C_1B \), \( \angle A_1O_1B = \angle C_1O_1B = \frac{1}{2} \angle A_1O_1C_1 = \frac{1}{2} \angle MBH \).
В прямоугольном треугольнике \(MBH\), тангенс угла \( \angle MBH \) равен отношению противолежащего катета к прилежащему: \( \text{tg} \angle MBH = \frac{MH}{BH} = \frac{\lambda R}{r} \).
Точка \(H\) является центром равностороннего треугольника \(A_1A_2A_3\). Расстояние от центра равностороннего треугольника до вершины равно \( \frac{\text{сторона}}{\sqrt{3}} \). Следовательно, \( A_1H = \frac{A_1A_2}{\sqrt{3}} = \frac{2R}{\sqrt{3}} = \frac{2\sqrt{3}R}{3} \).
Отрезок \(A_1B\) равен разности \(A_1H\) и \(BH\): \( A_1B = A_1H — BH = \frac{2\sqrt{3}R}{3} — r \).
Рассмотрим прямоугольный треугольник \(O_1A_1B\). Угол \( \angle A_1O_1B = \frac{1}{2} \angle MBH \). Тангенс этого угла равен отношению противолежащего катета \(A_1B\) к прилежащему катету \(O_1A_1\): \( \text{tg} \frac{\angle MBH}{2} = \frac{A_1B}{O_1A_1} = \frac{\frac{2\sqrt{3}}{3}R — r}{R} = \frac{2\sqrt{3}}{3} — \frac{r}{R} \).
Теперь используем формулу тангенса двойного угла: \( \text{tg} \angle MBH = \text{tg} \left( 2 \cdot \frac{\angle MBH}{2} \right) = \frac{2 \text{tg} \frac{\angle MBH}{2}}{1 — \text{tg}^2 \frac{\angle MBH}{2}} \).
Подставляем известные выражения для \( \text{tg} \angle MBH \) и \( \text{tg} \frac{\angle MBH}{2} \):
\( \frac{\lambda R}{r} = \frac{2 \left( \frac{2\sqrt{3}}{3} — \frac{r}{R} \right)}{1 — \left( \frac{2\sqrt{3}}{3} — \frac{r}{R} \right)^2} \)
\( \frac{\lambda R}{r} = \frac{\frac{4\sqrt{3}}{3} — \frac{2r}{R}}{1 — \left( \frac{12}{9} — \frac{4\sqrt{3}}{3} \frac{r}{R} + \frac{r^2}{R^2} \right)} \)
\( \frac{\lambda R}{r} = \frac{\frac{4\sqrt{3}}{3} — \frac{2r}{R}}{1 — \frac{4}{3} + \frac{4\sqrt{3}}{3} \frac{r}{R} — \frac{r^2}{R^2}} \)
\( \frac{\lambda R}{r} = \frac{\frac{4\sqrt{3}R — 6r}{3R}}{\frac{3R^2 — 4R^2 + 4\sqrt{3}Rr — 3r^2}{3R^2}} \)
\( \frac{\lambda R}{r} = \frac{4\sqrt{3}R — 6r}{3R} \cdot \frac{3R^2}{-R^2 + 4\sqrt{3}Rr — 3r^2} \)
\( \lambda R (-R^2 + 4\sqrt{3}Rr — 3r^2) = r (4\sqrt{3}R — 6r) R \)
\( -\lambda R^3 + 4\sqrt{3}\lambda R^2 r — 3\lambda R r^2 = 4\sqrt{3}R^2 r — 6Rr^2 \)
\( 3\lambda R r^2 — 6Rr^2 — 4\sqrt{3}\lambda R^2 r + 4\sqrt{3}R^2 r + \lambda R^3 = 0 \)
\( (3\lambda — 6)R r^2 — (4\sqrt{3}\lambda — 4\sqrt{3})R^2 r + \lambda R^3 = 0 \)
Делим на \(R\) (поскольку \(R \neq 0\)):
\( 3(\lambda — 2)r^2 — 4\sqrt{3}R(\lambda — 1)r + \lambda R^2 = 0 \)
Это квадратное уравнение относительно \(r\). Рассмотрим два случая для параметра \( \lambda \).
Случай 1: \( \lambda = 2 \).
Подставляем \( \lambda = 2 \) в уравнение:
\( 3(2 — 2)r^2 — 4\sqrt{3}R(2 — 1)r + 2R^2 = 0 \)
\( 0 \cdot r^2 — 4\sqrt{3}R(1)r + 2R^2 = 0 \)
\( -4\sqrt{3}Rr + 2R^2 = 0 \)
\( 4\sqrt{3}Rr = 2R^2 \)
\( r = \frac{2R^2}{4\sqrt{3}R} = \frac{R}{2\sqrt{3}} = \frac{R\sqrt{3}}{6} \).
Случай 2: \( \lambda \neq 2 \).
Используем формулу для корней квадратного уравнения \( ar^2 + br + c = 0 \), где \( a = 3(\lambda — 2) \), \( b = -4\sqrt{3}R(\lambda — 1) \), \( c = \lambda R^2 \).
Дискриминант \( D = b^2 — 4ac \):
\( D = (-4\sqrt{3}R(\lambda — 1))^2 — 4 \cdot 3(\lambda — 2) \cdot \lambda R^2 \)
\( D = 16 \cdot 3 R^2 (\lambda — 1)^2 — 12 \lambda R^2 (\lambda — 2) \)
\( D = 48 R^2 (\lambda^2 — 2\lambda + 1) — 12 \lambda R^2 (\lambda — 2) \)
\( D = 48 R^2 \lambda^2 — 96 R^2 \lambda + 48 R^2 — 12 \lambda^2 R^2 + 24 \lambda R^2 \)
\( D = 36 R^2 \lambda^2 — 72 R^2 \lambda + 48 R^2 \)
\( D = 12 R^2 (3\lambda^2 — 6\lambda + 4) \)
Корни уравнения: \( r = \frac{-b \pm \sqrt{D}}{2a} \)
\( r = \frac{4\sqrt{3}R(\lambda — 1) \pm \sqrt{12 R^2 (3\lambda^2 — 6\lambda + 4)}}{2 \cdot 3(\lambda — 2)} \)
\( r = \frac{4\sqrt{3}R(\lambda — 1) \pm 2R\sqrt{3 (3\lambda^2 — 6\lambda + 4)}}{6(\lambda — 2)} \)
\( r = \frac{4\sqrt{3}R(\lambda — 1) \pm 2R\sqrt{9\lambda^2 — 18\lambda + 12}}{6(\lambda — 2)} \)
\( r = \frac{2\sqrt{3}R(\lambda — 1) \pm R\sqrt{9\lambda^2 — 18\lambda + 12}}{3(\lambda — 2)} \)
\( r = R \cdot \frac{2\sqrt{3}(\lambda — 1) \pm \sqrt{9\lambda^2 — 18\lambda + 12}}{3(\lambda — 2)} \)
Из геометрических соображений радиус основания конуса \(r\) должен быть меньше \(A_1H\), то есть \( r < \frac{2\sqrt{3}}{3}R \). Также, чтобы конус существовал, \(r > 0\).
Рассмотрим знак числителя \( 2\sqrt{3}(\lambda — 1) \pm \sqrt{9\lambda^2 — 18\lambda + 12} \).
Дискриминант \( 9\lambda^2 — 18\lambda + 12 \) имеет дискриминант \( (-18)^2 — 4 \cdot 9 \cdot 12 = 324 — 432 = -108 < 0 \). Поскольку коэффициент при \( \lambda^2 \) положительный (9), выражение \( 9\lambda^2 - 18\lambda + 12 \) всегда положительно, и корень из него всегда действителен. Сравнивая с ответом в примере, выбираем знак минус перед корнем.
\( r = R \cdot \frac{2\sqrt{3}(\lambda - 1) - \sqrt{9\lambda^2 - 18\lambda + 12}}{3(\lambda - 2)} \). Ответ: \( r = R \cdot \frac{2\sqrt{3}(\lambda - 1) - \sqrt{9\lambda^2 - 18\lambda + 12}}{3(\lambda - 2)} \) при \( \lambda \neq 2 \); \( r = \frac{R\sqrt{3}}{6} \) при \( \lambda = 2 \).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.