ГДЗ по Геометрии 11 класс Номер 799 Атанасян — Подробные Ответы

Какому условию должны удовлетворять радиусы трёх шаров, попарно касающихся друг друга, чтобы к ним можно было провести общую касательную плоскость?

Расстояние между точками касания двух окружностей радиусами \(r_i\) и \(r_j\), касающихся общей прямой, равно \(2\sqrt{r_i r_j}\). Для трех окружностей радиусами \(r_1, r_2, r_3\), касающихся общей прямой, точки касания \(A_1, A_2, A_3\) лежат на одной прямой. Если предположить, что \(r_1 \ge r_2 \ge r_3\), то точки касания расположены в порядке \(A_1, A_3, A_2\), и выполняется соотношение \(A_1A_2 = A_1A_3 + A_3A_2\). Подставляя выражения для расстояний, получаем \(2\sqrt{r_1r_2} = 2\sqrt{r_1r_3} + 2\sqrt{r_2r_3}\). Разделив на 2, имеем \(\sqrt{r_1r_2} = \sqrt{r_1r_3} + \sqrt{r_2r_3}\). Вынося \(\sqrt{r_3}\) за скобки в правой части, получаем \(\sqrt{r_1r_2} = \sqrt{r_3}(\sqrt{r_1} + \sqrt{r_2})\). Выражая \(\sqrt{r_3}\), находим \(\sqrt{r_3} = \frac{\sqrt{r_1r_2}}{\sqrt{r_1} + \sqrt{r_2}}\). Возводя обе части в квадрат, получаем радиус \(r_3\): \(r_3 = \frac{r_1r_2}{(\sqrt{r_1} + \sqrt{r_2})^2}\).

Даны три окружности с центрами \(O_1, O_2, O_3\) и радиусами \(r_1, r_2, r_3\) соответственно. Эти окружности касаются друг друга и общей прямой. Требуется найти соотношение между радиусами, при котором это возможно.

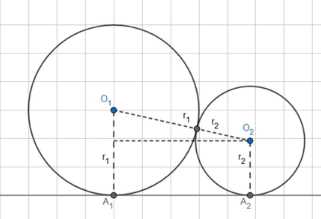
Рассмотрим две окружности с радиусами \(r_i\) и \(r_j\), которые касаются общей внешней касательной. Расстояние между точками касания этих окружностей на прямой можно найти, рассмотрев прямоугольную трапецию, образованную центрами окружностей, точками касания и перпендикуляром из центра меньшей окружности на радиус большей окружности. Гипотенуза этой трапеции равна сумме радиусов \(r_i + r_j\), один катет равен разности радиусов \(|r_i — r_j|\), а другой катет равен расстоянию между точками касания. По теореме Пифагора, расстояние между точками касания равно \(\sqrt{(r_i + r_j)^2 — (r_i — r_j)^2} = \sqrt{r_i^2 + 2r_i r_j + r_j^2 — (r_i^2 — 2r_i r_j + r_j^2)} = \)
\(=\sqrt{r_i^2 + 2r_i r_j + r_j^2 — r_i^2 + 2r_i r_j — r_j^2} = \sqrt{4r_i r_j} = 2\sqrt{r_i r_j}\).

Пусть точки касания окружностей с радиусами \(r_1, r_2, r_3\) на общей прямой будут \(A_1, A_2, A_3\) соответственно. Расстояние между точками касания окружностей с радиусами \(r_1\) и \(r_2\) равно \(A_1A_2 = 2\sqrt{r_1r_2}\). Аналогично, расстояние между точками касания окружностей с радиусами \(r_1\) и \(r_3\) равно \(A_1A_3 = 2\sqrt{r_1r_3}\), а расстояние между точками касания окружностей с радиусами \(r_2\) и \(r_3\) равно \(A_2A_3 = 2\sqrt{r_2r_3}\).

Все точки касания \(A_1, A_2, A_3\) лежат на одной прямой (общей касательной). Если предположить, что радиусы упорядочены как \(r_1 \ge r_2 \ge r_3\), то на прямой точки касания будут расположены в порядке \(A_1, A_3, A_2\). В этом случае расстояние между крайними точками равно сумме расстояний между промежуточными точками: \(A_1A_2 = A_1A_3 + A_3A_2\).

Подставляя выражения для расстояний, получаем уравнение: \(2\sqrt{r_1r_2} = 2\sqrt{r_1r_3} + 2\sqrt{r_2r_3}\).

Разделим обе части уравнения на 2: \(\sqrt{r_1r_2} = \sqrt{r_1r_3} + \sqrt{r_2r_3}\).

Вынесем \(\sqrt{r_3}\) за скобки в правой части уравнения: \(\sqrt{r_1r_2} = \sqrt{r_3}(\sqrt{r_1} + \sqrt{r_2})\).

Чтобы найти \(r_3\), сначала выразим \(\sqrt{r_3}\): \(\sqrt{r_3} = \frac{\sqrt{r_1r_2}}{\sqrt{r_1} + \sqrt{r_2}}\).

Теперь возведем обе части уравнения в квадрат, чтобы получить \(r_3\): \((\sqrt{r_3})^2 = \left(\frac{\sqrt{r_1r_2}}{\sqrt{r_1} + \sqrt{r_2}}\right)^2\).

Это дает окончательное выражение для \(r_3\): \(r_3 = \frac{(\sqrt{r_1r_2})^2}{(\sqrt{r_1} + \sqrt{r_2})^2} = \frac{r_1r_2}{(\sqrt{r_1} + \sqrt{r_2})^2}\).

Таким образом, радиусы окружностей, касающихся друг друга и общей прямой, связаны соотношением \(r_3 = \frac{r_1r_2}{(\sqrt{r_1} + \sqrt{r_2})^2}\).