ГДЗ по Геометрии 11 класс Номер 798 Атанасян — Подробные Ответы

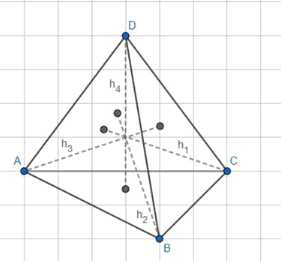
В тетраэдр с высотами \(h_1, h_2, h_3, h_4\) вписан шар радиуса R. Докажите, что \(R = \frac{1}{h_1} + \frac{1}{h_2} + \frac{1}{h_3} + \frac{1}{h_4})\).

Объем данного тетраэдра равен \( V = \frac{1}{3} S_i h_i \), где \( S_i \) — площадь \(i\)-й грани, а \( h_i \) — высота, опущенная на эту грань. Отсюда следует, что \( \frac{S_i}{3} = \frac{V}{h_i} \) для \( i = 1, 2, 3, 4 \). Точка \(O\), центр вписанной сферы радиуса \(R\), делит тетраэдр на четыре меньших тетраэдра, основаниями которых являются грани исходного тетраэдра, а высоты равны \(R\). Объем исходного тетраэдра равен сумме объемов этих четырех тетраэдров: \( V = \frac{1}{3} S_1 R + \frac{1}{3} S_2 R + \frac{1}{3} S_3 R + \frac{1}{3} S_4 R = \sum_{i=1}^{4} \frac{1}{3} S_i R \). Подставляя выражение для \( \frac{1}{3} S_i \) из первого соотношения, получаем \( V = \sum_{i=1}^{4} \frac{V}{h_i} R = VR \sum_{i=1}^{4} \frac{1}{h_i} \). Поскольку \( V \neq 0 \), можно разделить обе части на \( VR \), откуда следует \( \frac{1}{R} = \sum_{i=1}^{4} \frac{1}{h_i} \), что равносильно \( \frac{1}{R} = \frac{1}{h_1} + \frac{1}{h_2} + \frac{1}{h_3} + \frac{1}{h_4} \). Это и требовалось доказать.

Дано: тетраэдр с высотами \(h_1, h_2, h_3, h_4\), опущенными на соответствующие грани, и вписанная сфера с центром \(O\) и радиусом \(R\).
Требуется доказать: \( \frac{1}{R} = \frac{1}{h_1} + \frac{1}{h_2} + \frac{1}{h_3} + \frac{1}{h_4} \).

Доказательство:
Объем \(V\) данного тетраэдра может быть выражен через площадь любой его грани \(S_i\) и соответствующую высоту \(h_i\), опущенную на эту грань, по формуле \( V = \frac{1}{3} S_i h_i \), где \(i\) принимает значения от 1 до 4, обозначая каждую из четырех граней тетраэдра. Из этой формулы мы можем выразить отношение площади грани к трем: \( \frac{S_i}{3} = \frac{V}{h_i} \). Это соотношение будет использовано далее.

Точка \(O\), являющаяся центром вписанной сферы, находится на одинаковом расстоянии \(R\) от всех граней тетраэдра. Эта точка делит исходный тетраэдр на четыре меньших тетраэдра. Основанием каждого из этих меньших тетраэдров является одна из граней исходного тетраэдра, а вершиной является точка \(O\). Высота каждого такого меньшего тетраэдра, опущенная из вершины \(O\) на соответствующую грань, равна радиусу вписанной сферы \(R\).

Объем исходного тетраэдра \(V\) равен сумме объемов этих четырех меньших тетраэдров. Объем \(i\)-го меньшего тетраэдра с основанием \(S_i\) и высотой \(R\) равен \( \frac{1}{3} S_i R \). Следовательно, общий объем тетраэдра выражается как сумма объемов этих четырех тетраэдров:
\( V = \frac{1}{3} S_1 R + \frac{1}{3} S_2 R + \frac{1}{3} S_3 R + \frac{1}{3} S_4 R \).
Эту сумму можно записать с использованием знака суммирования:
\( V = \sum_{i=1}^{4} \frac{1}{3} S_i R \).

Теперь подставим в эту формулу выражение для \( \frac{1}{3} S_i \) из соотношения \( \frac{S_i}{3} = \frac{V}{h_i} \), полученного в начале доказательства. Заменяя \( \frac{1}{3} S_i \) на \( \frac{V}{h_i} \), получаем:
\( V = \sum_{i=1}^{4} \frac{V}{h_i} R \).
Вынесем общие множители \(V\) и \(R\) за знак суммирования:
\( V = VR \sum_{i=1}^{4} \frac{1}{h_i} \).

Поскольку объем тетраэдра \(V\) не равен нулю, мы можем разделить обе части этого уравнения на \(V\). Получаем:
\( 1 = R \sum_{i=1}^{4} \frac{1}{h_i} \).
Разделив обе части на \(R\), окончательно получаем:
\( \frac{1}{R} = \sum_{i=1}^{4} \frac{1}{h_i} \).
Расписывая сумму, получаем требуемое соотношение:
\( \frac{1}{R} = \frac{1}{h_1} + \frac{1}{h_2} + \frac{1}{h_3} + \frac{1}{h_4} \).

Таким образом, мы доказали, что величина, обратная радиусу вписанной сферы тетраэдра, равна сумме величин, обратных длинам высот тетраэдра, опущенных на его грани.