Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 797 Атанасян — Подробные Ответы
Найдите множество всех таких точек, из которых можно провести к данной сфере три попарно перпендикулярные касательные прямые
Дано: сфера с центром в точке \(O\) радиуса \(R\).
Найти: все точки, из которых можно провести к сфере три перпендикулярные касательные.
Решение:
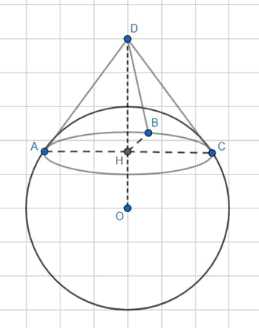
Рассмотрим точку \(D\) — одну из подходящих точек. Касательные, проведенные из этой точки \(DA\), \(DB\) и \(DC\).
Поскольку \(AO = OB = OC = R\) и \(OA \perp DA\), \(OB \perp DB\), \(OC \perp DC\), а \(DO\) — общая гипотенуза, то \(\triangle ADO = \triangle BDO = \triangle CDO\). Следовательно, \(DA = DB = DC\). Также \(\triangle ADB = \triangle BDC = \triangle ADC\), поэтому \(AB = BC = AC\).
Отметим точку \(H\) — центр \(\triangle ABC\). В правильной призме \(ABCD\): \(DH \perp ABC\) и \(OH \perp ABC\), значит \(H \in DO\).
В прямоугольном \(\triangle ABD\): \(AB = \sqrt{AD^2 + BD^2} = \sqrt{2AD^2} = DA\sqrt{2}\). Пусть \(DA = a\), тогда \(AB = a\sqrt{2}\).
В равностороннем \(\triangle ABC\): \(AH = R_{опис}\); \(AB = AH\sqrt{3}\); \(AH = \frac{AB}{\sqrt{3}} = \frac{a\sqrt{2}}{\sqrt{3}}\).
Прямоугольные треугольники \(\triangle ODA \sim \triangle HAD\), поэтому \(\frac{R_{сф}}{DO} = \frac{AH}{AD} = \frac{a\sqrt{2}}{a\sqrt{3}}\). Отсюда \(DO = \frac{\sqrt{3}R}{\sqrt{2}} = \frac{1}{2}R\sqrt{6}\).
Множеством всех таких точек является сфера, центр которой совпадает с центром данной сферы, радиус равен \(R\sqrt{6}/2\).
on the line passing through \(H\) and perpendicular to the plane \((ABC)\) because \(A,B,C\) are points of tangencyЗадача состоит в том, чтобы найти геометрическое место точек \(D\), из которых можно провести три взаимно перпендикулярные касательные к данной сфере с центром в точке \(O\) и радиусом \(R\).
Пусть \(D\) — одна из таких искомых точек. Проведем из точки \(D\) три касательные \(DA\), \(DB\) и \(DC\) к сфере. Точки \(A\), \(B\) и \(C\) являются точками касания. По условию задачи, эти три касательные взаимно перпендикулярны, то есть \(DA \perp DB\), \(DB \perp DC\) и \(DC \perp DA\).
Радиусы сферы, проведенные в точки касания, перпендикулярны касательным. Таким образом, \(OA \perp DA\), \(OB \perp DB\) и \(OC \perp DC\). Длины этих радиусов равны \(R\): \(OA = OB = OC = R\).
Рассмотрим прямоугольные треугольники \(\triangle OAD\), \(\triangle OBD\) и \(\triangle OCD\). У них прямой угол соответственно при вершинах \(A\), \(B\) и \(C\). Все эти три треугольника имеют
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.