
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 796 Атанасян — Подробные Ответы
Найдите множество центров всех сечений шара плоскостями, проходящими через данную прямую, не пересекающую шар.
Множеством центров всех сечений шара плоскостями, проходящими через прямую \(a\), является дуга окружности, расположенная внутри шара. Диаметр этой окружности равен расстоянию от центра шара \(O\) до прямой \(a\), а плоскость окружности перпендикулярна прямой \(a\).
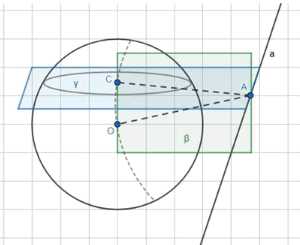
Рассмотрим произвольную плоскость \(\gamma\) проходящую через прямую \(a\), которая не пересекает шар с центром \(O\). Эта плоскость \(\gamma\) пересекает шар по окружности, если расстояние от центра шара до плоскости меньше радиуса шара. Пусть \(C\) — центр этой окружности сечения.
Отметим точку \(A\) на прямой \(a\) такую, что \(OA\) перпендикулярно \(a\). Поскольку прямая \(a\) не пересекает шар, точка \(A\) находится вне шара, и расстояние \(OA\) больше радиуса шара \(R\), то есть \(OA > R\). Плоскость, проходящая через центр шара \(O\) и перпендикулярная прямой \(a\), содержит точку \(A\). Обозначим эту плоскость как \(\beta\).
Центр \(C\) сечения лежит в плоскости \(\gamma\). Также известно, что отрезок, соединяющий центр шара \(O\) с центром сечения \(C\), перпендикулярен плоскости сечения \(\gamma\). Следовательно, \(OC \perp \gamma\). Поскольку прямая \(a\) лежит в плоскости \(\gamma\), \(OC\) перпендикулярно любой прямой в плоскости \(\gamma\), проходящей через \(C\). В частности, если \(AC\) лежит в \(\gamma\), то \(OC \perp AC\).
Рассмотрим треугольник \(OCA\). Угол \(\angle OCA\) является прямым, \(\angle OCA = 90^\circ\), так как \(OC \perp \gamma\) и \(AC \subset \gamma\). По свойству прямоугольного треугольника, вершина прямого угла \(C\) лежит на окружности с диаметром, равным гипотенузе \(OA\).
Таким образом, все центры \(C\) возможных сечений лежат на окружности с диаметром \(OA\). Эта окружность расположена в плоскости \(\beta\), которая проходит через \(O\) и перпендикулярна прямой \(a\).
Однако, сечение шара плоскостью существует только тогда, когда расстояние от центра шара до плоскости меньше радиуса шара. Это расстояние равно \(OC\). Следовательно, центры сечений \(C\) должны удовлетворять условию \(OC < R\). Поскольку \(OA > R\), не все точки окружности с диаметром \(OA\) соответствуют реальным сечениям. Множество центров сечений — это часть окружности с диаметром \(OA\), расположенная внутри шара. Эта часть окружности является дугой.
Итак, множеством центров всех сечений шара плоскостями, проходящими через прямую \(a\), является дуга окружности, расположенная внутри шара. Диаметр этой окружности равен расстоянию от центра шара \(O\) до прямой \(a\) (равному \(OA\)), а плоскость, в которой лежит эта окружность, перпендикулярна прямой \(a\) и проходит через центр шара \(O\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!