
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 795 Атанасян — Подробные Ответы
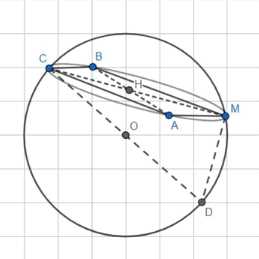
Из точки сферы проведены три попарно перпендикулярные хорды. Докажите, что сумма их квадратов не зависит от положения этих хорд.
Из \(\angle BMA = 90^\circ\) следует, что AB является диаметром сферы. В прямоугольном треугольнике ABM по теореме Пифагора имеем \(AB^2 = MA^2 + MB^2\). Так как \(MD \perp MA\) и \(MD \perp MB\), то \(MD\) перпендикулярно плоскости MAB. Из \(\angle CMD = 90^\circ\) следует, что CD является диаметром сферы. В прямоугольном треугольнике CMD по теореме Пифагора имеем \(CD^2 = MC^2 + MD^2\). Достраивая треугольник ABM до прямоугольника MABC, получаем \(MC = AB\). Подставляя это в выражение для \(CD^2\), имеем \(CD^2 = AB^2 + MD^2\). Далее, подставляя \(AB^2 = MA^2 + MB^2\), получаем \(CD^2 = (MA^2 + MB^2) + MD^2\). Поскольку CD — диаметр сферы, его длина постоянна, следовательно, \(CD^2\) постоянно. Таким образом, \(MA^2 + MB^2 + MD^2\) не изменяется.
Дано: шар с центром \(O\); хорды \(MA \perp MB \perp MD\). Доказать: \(MA^2 + MB^2 + MD^2\) не изменяется.
Доказательство:
Так как хорды \(MA\) и \(MB\) перпендикулярны, \(\angle BMA = 90^\circ\). Угол, опирающийся на диаметр сферы, равен \(90^\circ\). Поскольку точки \(M\), \(B\), \(A\) лежат на сфере и \(\angle BMA = 90^\circ\), отрезок \(AB\) является диаметром сферы. В прямоугольном треугольнике \(AMB\) по теореме Пифагора имеем \(AB^2 = MA^2 + MB^2\).
Достроим треугольник \(ABM\) до прямоугольника \(MABC\). В прямоугольнике противоположные стороны равны, поэтому \(MC = AB\). Возводя обе части в квадрат, получаем \(MC^2 = AB^2\). Подставляя сюда выражение для \(AB^2\) из предыдущего шага, имеем \(MC^2 = MA^2 + MB^2\). Поскольку \(M\), \(A\), \(B\) лежат на сфере и \(AB\) является диаметром, точка \(C\), построенная таким образом, также лежит на сфере, и отрезок \(MC\) является диаметром сферы.
Так как хорды \(MD\) и \(MC\) являются диаметрами сферы, и они выходят из одной точки \(M\), это означает, что \(C\) и \(D\) являются точками, диаметрально противоположными \(M\). Следовательно, точки \(C\) и \(D\) совпадают. Однако, по условию даны три взаимно перпендикулярные хорды \(MA\), \(MB\), \(MD\), выходящие из точки \(M\), что подразумевает три различных направления.
Возможно, в шаге 2 имеется в виду построение точки \(C\) такой, что \(MABC\) является прямоугольником, и эта точка \(C\) лежит на сфере. Если \(M\), \(A\), \(B\) на сфере и \(AB\) диаметр, то точка \(C\) такая, что \(MABC\) — прямоугольник, будет на сфере, и \(MC\) будет диаметром.
Рассмотрим шаг 5 доказательства из примера: \(\angle CMD = 90^\circ\). Если точки \(M\), \(C\), \(D\) лежат на сфере и \(\angle CMD = 90^\circ\), то отрезок \(CD\) является диаметром сферы. В прямоугольном треугольнике \(CMD\) по теореме Пифагора имеем \(CD^2 = MC^2 + MD^2\).
Теперь подставим выражение для \(MC^2\) из шага 2 (\(MC^2 = AB^2\)): \(CD^2 = AB^2 + MD^2\).
Далее, подставим выражение для \(AB^2\) из шага 1 (\(AB^2 = MA^2 + MB^2\)): \(CD^2 = (MA^2 + MB^2) + MD^2\).
Таким образом, \(CD^2 = MA^2 + MB^2 + MD^2\). Поскольку \(CD\) является диаметром сферы, его длина постоянна для данной сферы. Следовательно, \(CD^2\) является постоянной величиной. Это означает, что сумма квадратов длин хорд \(MA^2 + MB^2 + MD^2\) не изменяется.
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!