
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 794 Атанасян — Подробные Ответы
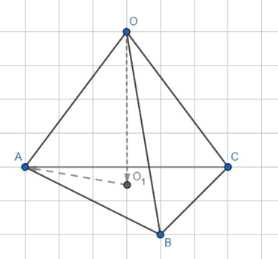
Все плоские углы тетраэдра ОАВС при вершине О прямые. Докажите, что проекция вершины О на плоскость АВС есть точка пересечения высот треугольника АВС
Обозначим ребра тетраэдра OABC как векторы. Тогда \(\vec{BC} = \vec{OC} — \vec{OB}\) и \(\vec{O_1A} = \vec{OA} — \vec{OO_1}\). Из условия \(AOB \perp BOC \perp COA\) следует, что \(\vec{OA} \perp \vec{OC}\) и \(\vec{OA} \perp \vec{OB}\). Точка \(O_1\) получается из \(O\) перемещением, перпендикулярным плоскости ABC, то есть \(\vec{OO_1} \perp ABC\), откуда следует, что \(\vec{BC} \perp \vec{OO_1}\). Вычислим скалярное произведение \(\vec{BC} \cdot \vec{O_1A} = (\vec{OC} — \vec{OB}) \cdot (\vec{OA} — \vec{OO_1}) = \vec{OC} \cdot \vec{OA} — \vec{OC} \cdot \vec{OO_1} -\)
\(- \vec{OB} \cdot \vec{OA} + \vec{OB} \cdot \vec{OO_1}\). Поскольку \(\vec{OC} \cdot \vec{OA} = 0\) и \(\vec{OB} \cdot \vec{OA} = 0\), получаем \(\vec{BC} \cdot \vec{O_1A} =-\vec{OC} \cdot \vec{OO_1} + \vec{OB} \cdot \vec{OO_1} = (\vec{OB} — \vec{OC}) \cdot \vec{OO_1} = \)
\(= -(\vec{OC} — \vec{OB}) \cdot \vec{OO_1} = -\vec{BC} \cdot \vec{OO_1}\). Так как \(\vec{BC} \perp \vec{OO_1}\), то \(\vec{BC} \cdot \vec{OO_1} = 0\), следовательно, \(\vec{BC} \cdot \vec{O_1A} = 0\), что означает \(\vec{BC} \perp \vec{O_1A}\). Аналогично доказывается, что \(\vec{O_1B} \perp \vec{AC}\) и \(\vec{O_1C} \perp \vec{AB}\). Таким образом, \(O_1A\), \(O_1B\), и \(O_1C\) являются высотами треугольника ABC, и поскольку они исходят из точки \(O_1\), эта точка является точкой пересечения высот треугольника ABC, что и требовалось доказать.
Обозначим радиус-векторы вершин тетраэдра относительно начала координат O как \(\vec{OA}\), \(\vec{OB}\), \(\vec{OC}\) и \(\vec{OO}\) (который является нулевым вектором). Векторы, представляющие ребра тетраэдра, могут быть выражены через разность радиус-векторов их конечной и начальной точек. Например, вектор \(\vec{BC}\), направленный из точки B в точку C, равен \(\vec{OC} — \vec{OB}\). Вектор \(\vec{O_1A}\), направленный из точки \(O_1\) в точку A, равен \(\vec{OA} — \vec{OO_1}\).
Из условия задачи дано, что ребра OA, OB, OC взаимно перпендикулярны. Это означает, что скалярные произведения векторов, направленных вдоль этих ребер, равны нулю: \(\vec{OA} \cdot \vec{OB} = 0\), \(\vec{OB} \cdot \vec{OC} = 0\), и \(\vec{OC} \cdot \vec{OA} = 0\). Также дано, что точка \(O_1\) такова, что вектор \(\vec{OO_1}\) перпендикулярен плоскости треугольника ABC. Если вектор перпендикулярен плоскости, он перпендикулярен любому вектору, лежащему в этой плоскости. Вектор \(\vec{BC}\) лежит в плоскости ABC, следовательно, \(\vec{OO_1}\) перпендикулярен \(\vec{BC}\), что означает \(\vec{OO_1} \cdot \vec{BC} = 0\).
Рассмотрим скалярное произведение вектора \(\vec{BC}\) и вектора \(\vec{O_1A}\). Используя векторные представления, полученные в первом шаге, имеем:
\(\vec{BC} \cdot \vec{O_1A} = (\vec{OC} — \vec{OB}) \cdot (\vec{OA} — \vec{OO_1})\).
Применяя свойство дистрибутивности скалярного произведения, раскроем скобки:
\((\vec{OC} — \vec{OB}) \cdot (\vec{OA} — \vec{OO_1}) = \vec{OC} \cdot \vec{OA} — \vec{OC} \cdot \vec{OO_1} — \vec{OB} \cdot \vec{OA} + \vec{OB} \cdot \vec{OO_1}\).
Из условия взаимной перпендикулярности ребер OA, OB, OC мы знаем, что \(\vec{OC} \cdot \vec{OA} = 0\) и \(\vec{OB} \cdot \vec{OA} = 0\). Подставляя эти значения в выражение, получаем:
\(0 — \vec{OC} \cdot \vec{OO_1} — 0 + \vec{OB} \cdot \vec{OO_1} = \vec{OB} \cdot \vec{OO_1} — \vec{OC} \cdot \vec{OO_1}\).
Вынесем общий множитель \(\vec{OO_1}\):
\(\vec{OB} \cdot \vec{OO_1} — \vec{OC} \cdot \vec{OO_1} = (\vec{OB} — \vec{OC}) \cdot \vec{OO_1}\).
Заметим, что \(\vec{OB} — \vec{OC} = -(\vec{OC} — \vec{OB}) = -\vec{BC}\). Следовательно, выражение равно:
\((-\vec{BC}) \cdot \vec{OO_1} = -\vec{BC} \cdot \vec{OO_1}\).
Ранее мы установили, что \(\vec{BC} \perp \vec{OO_1}\), что означает \(\vec{BC} \cdot \vec{OO_1} = 0\).
Таким образом, \(\vec{BC} \cdot \vec{O_1A} = -\vec{BC} \cdot \vec{OO_1} = -0 = 0\).
Скалярное произведение векторов \(\vec{BC}\) и \(\vec{O_1A}\) равно нулю, что доказывает их перпендикулярность: \(\vec{BC} \perp \vec{O_1A}\). Это означает, что отрезок \(O_1A\) перпендикулярен стороне BC треугольника ABC. Поскольку \(O_1A\) соединяет вершину A с точкой \(O_1\), это показывает, что отрезок \(O_1A\) лежит на высоте треугольника ABC, проведенной из вершины A к стороне BC.
Аналогичные рассуждения можно провести для других сторон треугольника ABC. Вычисляя скалярное произведение \(\vec{AC} \cdot \vec{O_1B}\) и \(\vec{AB} \cdot \vec{O_1C}\) и используя условия взаимной перпендикулярности ребер OA, OB, OC и перпендикулярности \(\vec{OO_1}\) плоскости ABC, можно показать, что \(\vec{AC} \cdot \vec{O_1B} = 0\) и \(\vec{AB} \cdot \vec{O_1C} = 0\). Это доказывает, что \(\vec{O_1B} \perp \vec{AC}\) и \(\vec{O_1C} \perp \vec{AB}\). Следовательно, отрезки \(O_1B\) и \(O_1C\) лежат на высотах треугольника ABC, проведенных из вершин B и C соответственно.
Поскольку точка \(O_1\) лежит на всех трех высотах треугольника ABC (отрезки \(O_1A\), \(O_1B\), \(O_1C\) являются частями или продолжениями высот), она является точкой их пересечения. Точка пересечения высот треугольника называется ортоцентром. Таким образом, точка \(O_1\) является точкой пересечения высот треугольника ABC, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!