ГДЗ по Геометрии 11 класс Номер 793 Атанасян — Подробные Ответы

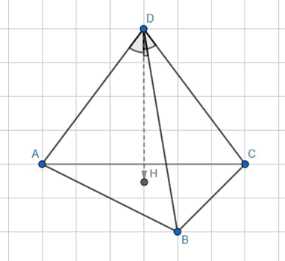
Три боковых ребра тетраэдра равны друг другу. Докажите, что прямая, образующая равные углы с этими рёбрами и пересекающая плоскость основания, перпендикулярна к этой плоскости.

Обозначим ребра тетраэдра как векторы: \( \vec{DA} \cdot \vec{DH} = \vec{DB} \cdot \vec{DH} = \vec{DC} \cdot \vec{DH} = a \cdot DH \cdot \cos \phi \). Из этого следует \( \vec{DB} \cdot \vec{DH} — \vec{DA} \cdot \vec{DH} = 0 \) и \( \vec{DC} \cdot \vec{DH} — \vec{DA} \cdot \vec{DH} = 0 \). Преобразуем: \( (\vec{DB} — \vec{DA}) \cdot \vec{DH} = 0 \), что означает \( \vec{AB} \cdot \vec{DH} = 0 \), следовательно \( DH \perp AB \). Аналогично, \( (\vec{DC} — \vec{DA}) \cdot \vec{DH} = 0 \), что означает \( \vec{AC} \cdot \vec{DH} = 0 \), следовательно \( DH \perp AC \). Поскольку прямая \(DH\) перпендикулярна двум пересекающимся прямым \(AB\) и \(AC\) в плоскости \(ABC\), то \(DH\) перпендикулярна плоскости \(ABC\). Что и требовалось доказать.

Дано: тетраэдр \(ABCD\), \(AD = BD = CD = a\), \(DH \cap ABC = H\), \( \angle ADH = \angle BDH = \angle CDH = \phi \).
Доказать: \( DH \perp ABC \).

Доказательство:
Первый шаг доказательства заключается в использовании векторов и скалярного произведения. Обозначим ребра тетраэдра как векторы. Из условия \(AD = BD = CD = a\) и \( \angle ADH = \angle BDH = \angle CDH = \phi \) следует, что скалярные произведения векторов \( \vec{DA} \), \( \vec{DB} \), \( \vec{DC} \) на вектор \( \vec{DH} \) равны. По определению скалярного произведения, \( \vec{DA} \cdot \vec{DH} = |\vec{DA}| \cdot |\vec{DH}| \cdot \cos(\angle ADH) = a \cdot DH \cdot \cos \phi \). Аналогично, \( \vec{DB} \cdot \vec{DH} = |\vec{DB}| \cdot |\vec{DH}| \cdot \cos(\angle BDH) = a \cdot DH \cdot \cos \phi \) и \( \vec{DC} \cdot \vec{DH} = |\vec{DC}| \cdot |\vec{DH}| \cdot \cos(\angle CDH) = a \cdot DH \cdot \cos \phi \). Таким образом, имеем равенство скалярных произведений: \( \vec{DA} \cdot \vec{DH} = \vec{DB} \cdot \vec{DH} = \vec{DC} \cdot \vec{DH} = a \cdot DH \cdot \cos \phi \).

Рассмотрим равенство \( \vec{DB} \cdot \vec{DH} = \vec{DA} \cdot \vec{DH} \). Перенесем все члены в одну сторону: \( \vec{DB} \cdot \vec{DH} — \vec{DA} \cdot \vec{DH} = 0 \). Используя свойство дистрибутивности скалярного произведения, получим \( (\vec{DB} — \vec{DA}) \cdot \vec{DH} = 0 \). Вектор разности \( \vec{DB} — \vec{DA} \) равен вектору \( \vec{AB} \). Следовательно, \( \vec{AB} \cdot \vec{DH} = 0 \). Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы ортогональны. Поскольку \( \vec{AB} \) и \( \vec{DH} \) являются векторами, соответствующими ребрам тетраэдра и высоте (или ее части), они не являются нулевыми векторами (если только тетраэдр не вырожденный, что не предполагается в стандартных геометрических задачах). Таким образом, \( \vec{AB} \) ортогонален \( \vec{DH} \), что означает, что прямая \(DH\) перпендикулярна прямой \(AB\), то есть \( DH \perp AB \).

Аналогично рассмотрим равенство \( \vec{DC} \cdot \vec{DH} = \vec{DA} \cdot \vec{DH} \). Перенесем члены: \( \vec{DC} \cdot \vec{DH} — \vec{DA} \cdot \vec{DH} = 0 \). Используя свойство дистрибутивности, получим \( (\vec{DC} — \vec{DA}) \cdot \vec{DH} = 0 \). Вектор разности \( \vec{DC} — \vec{DA} \) равен вектору \( \vec{AC} \). Следовательно, \( \vec{AC} \cdot \vec{DH} = 0 \). Это означает, что вектор \( \vec{AC} \) ортогонален вектору \( \vec{DH} \), что геометрически интерпретируется как перпендикулярность прямых \(DH\) и \(AC\), то есть \( DH \perp AC \).

Таким образом, мы установили, что прямая \(DH\) перпендикулярна прямой \(AB\) и прямая \(DH\) перпендикулярна прямой \(AC\). Прямые \(AB\) и \(AC\) лежат в плоскости \(ABC\) и пересекаются в точке \(A\). Согласно признаку перпендикулярности прямой и плоскости, если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости. Поскольку \(DH \perp AB\) и \(DH \perp AC\), а прямые \(AB\) и \(AC\) лежат в плоскости \(ABC\) и пересекаются, то прямая \(DH\) перпендикулярна плоскости \(ABC\). То есть, \( DH \perp ABC \).

Что и требовалось доказать.