Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 792 Атанасян — Подробные Ответы
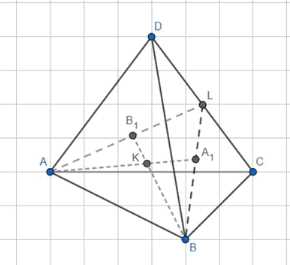
Докажите, что высоты тетраэдра пересекаются в одной точке тогда и только тогда, когда его противоположные рёбра перпендикулярны.
Доказательство: Если высоты тетраэдра \(ABCD\) пересекаются в точке \(K\), то из \(AA_1 \perp BCD\) и \(CD \in BCD\) следует \(AA_1 \perp CD\). Аналогично из \(BB_1 \perp ACD\) и \(CD \in ACD\) следует \(BB_1 \perp CD\). Поскольку \(AA_1\) и \(BB_1\) лежат в плоскости \(ALB\), то \(CD \perp ALB\), откуда \(CD \perp AB\). Аналогично доказывается перпендикулярность других пар противоположных ребер: \(BD \perp AC\) и \(DA \perp CB\). Обратное утверждение: Пусть противоположные ребра перпендикулярны, например \(DC \perp AB\). Так как \(AA_1 \perp BCD\) и \(DC \in BCD\), то \(AA_1 \perp DC\). Поскольку \(AB \perp DC\) и \(AA_1 \perp DC\), плоскость \(ABA_1\) перпендикулярна \(CD\). Высота \(BB_2\) треугольника \(ABL\) лежит в плоскости \(ABL\), которая совпадает с плоскостью \(ABA_1\), следовательно \(BB_2 \perp CD\). Также \(BB_2 \perp AL\). Таким образом, \(BB_2 \perp ACD\), и \(BB_2\) совпадает с высотой тетраэдра \(BB_1\). Высоты \(AA_1\) и \(BB_1\) пересекаются. Аналогично доказывается, что все высоты из соседних вершин пересекаются и не лежат в одной плоскости, то есть пересекаются в одной точке.
Дано: тетраэдр \(ABCD\); \(AA_1\), \(BB_1\), \(CC_1\), \(DD_1\) — высоты.
Доказать: высоты пересекаются в одной точке тогда и только тогда, когда его противоположные ребра перпендикулярны.
Доказательство:
Сначала докажем, что если высоты тетраэдра пересекаются в одной точке, то его противоположные ребра перпендикулярны.
Допустим, что высоты тетраэдра \(AA_1\), \(BB_1\), \(CC_1\), \(DD_1\) пересекаются в точке \(K\).
Высота \(AA_1\) перпендикулярна плоскости основания \(BCD\). Так как прямая \(CD\) лежит в плоскости \(BCD\), то по определению перпендикулярности прямой и плоскости, прямая \(AA_1\) перпендикулярна прямой \(CD\), то есть \(AA_1 \perp CD\).
Аналогично, высота \(BB_1\) перпендикулярна плоскости основания \(ACD\). Так как прямая \(CD\) лежит в плоскости \(ACD\), то по определению перпендикулярности прямой и плоскости, прямая \(BB_1\) перпендикулярна прямой \(CD\), то есть \(BB_1 \perp CD\).
Рассмотрим плоскость, проходящую через прямые \(AA_1\) и \(BB_1\). Согласно условию, высоты \(AA_1\) и \(BB_1\) пересекаются в точке \(K\), поэтому они лежат в одной плоскости. Пусть эта плоскость обозначена как \(ALB\), где \(L\) — точка пересечения прямой \(DC\) с этой плоскостью \(ABK\). Поскольку прямая \(CD\) перпендикулярна двум пересекающимся прямым \(AA_1\) и \(BB_1\), лежащим в плоскости \(ALB\), то прямая \(CD\) перпендикулярна плоскости \(ALB\).
Так как прямая \(AB\) лежит в плоскости \(ALB\), и прямая \(CD\) перпендикулярна плоскости \(ALB\), то по определению перпендикулярности прямой и плоскости, прямая \(CD\) перпендикулярна прямой \(AB\), то есть \(CD \perp AB\).
Аналогично, рассматривая другие пары высот, можно доказать, что другие пары противоположных ребер также перпендикулярны: \(BD \perp AC\) и \(DA \perp CB\).
Теперь докажем обратное утверждение: если противоположные ребра тетраэдра перпендикулярны, то его высоты пересекаются в одной точке.
Допустим, что противоположные ребра тетраэдра перпендикулярны, то есть \(DC \perp AB\), \(BD \perp AC\) и \(DA \perp CB\).
Рассмотрим высоту \(AA_1\) из вершины \(A\) на плоскость \(BCD\). По определению высоты, \(AA_1 \perp BCD\). Так как прямая \(DC\) лежит в плоскости \(BCD\), то \(AA_1 \perp DC\).
По условию нам дано, что \(AB \perp DC\).
Таким образом, прямая \(DC\) перпендикулярна двум пересекающимся прямым \(AA_1\) и \(AB\) в точке \(A\). Следовательно, прямая \(DC\) перпендикулярна плоскости, проходящей через эти прямые, то есть плоскости \(ABA_1\). Значит, \(ABA_1 \perp CD\).
Рассмотрим высоту \(BB_1\) из вершины \(B\) на плоскость \(ACD\).
Пусть \(BB_2\) — высота в треугольнике \(ABL\), где \(L\) — некоторая точка на прямой \(DC\), такая что плоскость \(ABL\) совпадает с плоскостью \(ABA_1\). Так как плоскость \(ABL\) (которая совпадает с \(ABA_1\)) перпендикулярна прямой \(CD\), и прямая \(BB_2\) лежит в плоскости \(ABL\), то \(BB_2 \perp CD\).
Поскольку \(BB_2\) является высотой треугольника \(ABL\), по определению высоты \(BB_2 \perp AL\).
Прямые \(AL\) и \(DC\) лежат в плоскости \(ACD\) (поскольку \(L\) лежит на \(DC\), и \(A, C, D\) определяют плоскость \(ACD\)). Прямая \(BB_2\) перпендикулярна прямой \(AL\) и прямой \(DC\). Если \(AL\) и \(DC\) являются пересекающимися прямыми в плоскости \(ACD\), то \(BB_2\) перпендикулярна плоскости \(ACD\). В данном случае \(L\) лежит на \(DC\), так что \(AL\) и \(DC\) могут пересекаться только в точке \(L\) if \(A, L, C\) are not collinear. Assuming a non-degenerate tetrahedron, \(AL\) and \(DC\) are not parallel and lie in \(ACD\), so they intersect at \(L\). Thus, \(BB_2 \perp ACD\).
Поскольку \(BB_2\) перпендикулярна плоскости \(ACD\) и проходит через вершину \(B\), \(BB_2\) является высотой тетраэдра из вершины \(B\) на плоскость \(ACD\), то есть \(BB_2\) совпадает с \(BB_1\).
Таким образом, высота \(BB_1\) лежит в плоскости \(ABA_1\). Поскольку высота \(AA_1\) также лежит в плоскости \(ABA_1\), и \(AA_1\) и \(BB_1\) не параллельны (они являются высотами из разных вершин к разным граням), то высоты \(AA_1\) и \(BB_1\) пересекаются.
Аналогично можно доказать, что любые две высоты, опущенные из соседних вершин, пересекаются.
Высоты тетраэдра, опущенные из разных вершин, не лежат в одной плоскости (для невырожденного тетраэдра). Если любые две высоты из соседних вершин пересекаются, и все высоты не лежат в одной плоскости, то они должны пересекаться в одной точке. Что и требовалось доказать.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.