
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 791 Атанасян — Подробные Ответы
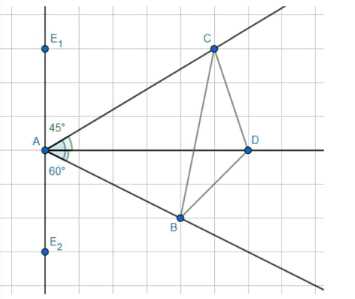
Из точки А исходят четыре луча AB, AC, AD и АЕ так, что \(\angle BAC = 60°\), \(\angle BAD = \angle DAC = 45°\), а луч АЕ перпендикулярен к плоскости ABD. Найдите угол САЕ.
В данном случае, дано, что \( \angle BAC = 60^\circ \), \( \angle BAD = 45^\circ \), \( \angle DAC = 45^\circ \). Также дано, что \( AE \) является лучом и \( AE \perp ABD \). Из условия \( CB \perp AB \) и \( AB = a \), в прямоугольном треугольнике \( \triangle ABC \) находим \( AC = 2AB = 2a \) и \( BC = \sqrt{AC^2 — AB^2} = \sqrt{(2a)^2 — a^2} = \sqrt{4a^2 — a^2} = \sqrt{3a^2} = a\sqrt{3} \). Из условия \( CD \perp AD \) и \( \angle DAC = 45^\circ \), в прямоугольном треугольнике \( \triangle ACD \) находим \( DC = AC \cdot \sin \angle DAC = 2a \cdot \sin 45^\circ = 2a \cdot \frac{\sqrt{2}}{2} = a\sqrt{2} \) и \( AD = \sqrt{AC^2 — CD^2} = \sqrt{(2a)^2 — (a\sqrt{2})^2} = \sqrt{4a^2 — 2a^2} = \sqrt{2a^2} = a\sqrt{2} \).
По теореме косинусов в \( \triangle ABD \): \( BD^2 = AB^2 + AD^2 — 2AB \cdot AD \cdot \cos \angle BAD = a^2 + (a\sqrt{2})^2 -\)
\(- 2a \cdot a\sqrt{2} \cdot \cos 45^\circ = a^2 + 2a^2 — 2a^2\sqrt{2} \cdot \frac{\sqrt{2}}{2} = 3a^2 — 2a^2 = a^2 \). Значит, \( BD = a \). В треугольнике \( \triangle BDC \), \( BC^2 = (a\sqrt{3})^2 = 3a^2 \), \( BD^2 = a^2 \), \( DC^2 = (a\sqrt{2})^2 = 2a^2 \). Так как \( BC^2 = BD^2 + DC^2 \), то \( \triangle BDC \) является прямоугольным с прямым углом при вершине \( D \), то есть \( CD \perp BD \). Поскольку \( CD \perp AD \) и \( CD \perp BD \), то \( CD \perp ABD \). Так как \( AE \perp ABD \), то \( DC \parallel AE \).
Если точки \( C \) и \( E \) лежат по одну сторону от прямой \( AD \), то \( \angle CAE = \angle ACD \). В прямоугольном треугольнике \( \triangle ACD \), \( \angle CAD = 45^\circ \), \( \angle ADC = 90^\circ \), следовательно, \( \angle ACD = 90^\circ — \angle CAD = 90^\circ — 45^\circ = 45^\circ \). Таким образом, \( \angle CAE = 45^\circ \).
Если точки \( C \) и \( E \) лежат по разные стороны от прямой \( AD \), то \( \angle CAE = 180^\circ — \angle ACD = 180^\circ — 45^\circ = 135^\circ \).
Ответ: 45° или 135°.
Дано: \( AB, AD, AC \) — отрезки, \( AE \) — луч, \( \angle BAC = 60^\circ \), \( \angle BAD = 45^\circ \), \( \angle DAC = 45^\circ \), \( AE \perp ABD \). Найти: \( \angle CAE \).
Первым шагом решения является определение положения точек \( B \) и \( D \) относительно точки \( A \) и заданных лучей. Введем обозначение \( AB = a \). Согласно условию, \( CB \perp AB \) и \( CD \perp AD \).
Рассмотрим прямоугольный треугольник \( \triangle ABC \). Угол \( \angle BAC = 60^\circ \). Поскольку \( \triangle ABC \) прямоугольный с прямым углом при вершине \( B \), то \( \angle ACB = 90^\circ — \angle BAC = 90^\circ — 60^\circ = 30^\circ \). Используя тригонометрические соотношения в прямоугольном треугольнике, находим длину \( AC \): \( \cos(\angle BAC) = \frac{AB}{AC} \), откуда \( AC = \frac{AB}{\cos(60^\circ)} = \frac{a}{1/2} = 2a \). Длину \( BC \) находим по теореме Пифагора: \( BC = \sqrt{AC^2 — AB^2} = \sqrt{(2a)^2 — a^2} = \sqrt{4a^2 — a^2} = \sqrt{3a^2} = a\sqrt{3} \).
Теперь рассмотрим прямоугольный треугольник \( \triangle ACD \). Угол \( \angle DAC = 45^\circ \). Поскольку \( \triangle ACD \) прямоугольный с прямым углом при вершине \( D \), то \( \angle ACD = 90^\circ — \angle DAC = 90^\circ — 45^\circ = 45^\circ \). Используя тригонометрические соотношения, находим длину \( DC \): \( \sin(\angle DAC) = \frac{DC}{AC} \), откуда \( DC = AC \cdot \sin(45^\circ) = 2a \cdot \frac{\sqrt{2}}{2} = a\sqrt{2} \). Длину \( AD \) находим по теореме Пифагора: \( AD = \sqrt{AC^2 — DC^2} = \sqrt{(2a)^2 — (a\sqrt{2})^2} = \sqrt{4a^2 — 2a^2} = \sqrt{2a^2} = a\sqrt{2} \). Заметим, что \( AD = DC = a\sqrt{2} \), и \( \triangle ACD \) является равнобедренным прямоугольным треугольником.
Далее, применим теорему косинусов к треугольнику \( \triangle ABD \) для нахождения длины \( BD \). Угол \( \angle BAD = 45^\circ \). По теореме косинусов: \( BD^2 = AB^2 + AD^2 — 2 \cdot AB \cdot AD \cdot \cos(\angle BAD) \). Подставляя известные значения: \( BD^2 = a^2 + (a\sqrt{2})^2 — 2 \cdot a \cdot a\sqrt{2} \cdot \cos(45^\circ) = a^2 + 2a^2 — 2a^2\sqrt{2} \cdot \frac{\sqrt{2}}{2} = \)
\(=3a^2 — 2a^2 \cdot 1 = 3a^2 — 2a^2 = a^2 \). Следовательно, \( BD = \sqrt{a^2} = a \).
Теперь рассмотрим треугольник \( \triangle BDC \). У нас есть длины всех его сторон: \( BC = a\sqrt{3} \), \( BD = a \), \( DC = a\sqrt{2} \). Проверим, выполняется ли теорема Пифагора для этих сторон: \( BD^2 + DC^2 = a^2 + (a\sqrt{2})^2 = a^2 + 2a^2 = 3a^2 \). Также \( BC^2 = (a\sqrt{3})^2 = 3a^2 \). Поскольку \( BD^2 + DC^2 = BC^2 \), по обратной теореме Пифагора, треугольник \( \triangle BDC \) является прямоугольным с прямым углом при вершине \( D \), то есть \( CD \perp BD \).
Мы установили, что \( CD \perp AD \) (по условию) и \( CD \perp BD \). Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна этой плоскости. Прямые \( AD \) и \( BD \) лежат в плоскости \( ABD \) и пересекаются в точке \( D \). Следовательно, \( CD \perp ABD \).
По условию задачи, луч \( AE \) перпендикулярен плоскости \( ABD \), то есть \( AE \perp ABD \). Поскольку и \( CD \perp ABD \), и \( AE \perp ABD \), то прямые \( CD \) и \( AE \) параллельны, то есть \( DC \parallel AE \).
Теперь рассмотрим возможные положения точки \( E \) относительно прямой \( AC \).
Случай 1: Точки \( C \) и \( E \) лежат по одну сторону от прямой \( AD \). Поскольку \( DC \parallel AE \), то угол между лучом \( AE \) и отрезком \( AC \) будет равен углу между отрезком \( DC \) и отрезком \( AC \). Таким образом, \( \angle CAE = \angle ACD \). Ранее мы нашли, что в прямоугольном треугольнике \( \triangle ACD \), \( \angle ACD = 45^\circ \). Следовательно, в этом случае \( \angle CAE = 45^\circ \).
Случай 2: Точки \( C \) и \( E \) лежат по разные стороны от прямой \( AD \). Поскольку \( DC \parallel AE \), то углы \( \angle CAE \) и \( \angle ACD \) являются смежными углами при параллельных прямых \( DC \) и \( AE \) и секущей \( AC \). В этом случае сумма этих углов равна \( 180^\circ \). Таким образом, \( \angle CAE + \angle ACD = 180^\circ \), откуда \( \angle CAE = 180^\circ — \angle ACD \). Используя найденное значение \( \angle ACD = 45^\circ \), получаем \( \angle CAE = 180^\circ — 45^\circ = 135^\circ \).
Таким образом, возможны два значения для угла \( \angle CAE \).
Ответ: 45° или 135°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!