Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 790 Атанасян — Подробные Ответы
Основание АВС тетраэдра ОАВС прозрачное, а все остальные грани зеркальные. Все плоские углы при вершине О прямые. Докажите, что луч света, вошедший в тетраэдр через основание АВС под произвольным углом к нему, отразившись от граней, выйдет в противоположном направлении по отношению к входящему лучу. (На этом свойстве основано устройство уголкового отражателя, который, в частности, был запущен на Луну для измерения расстояния до неё с помощью лазера.)
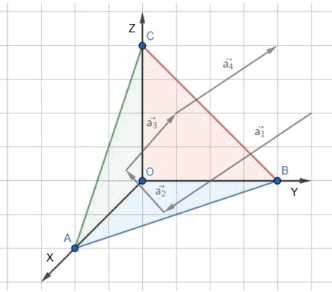
Введем систему координат с началом в точке О и осями ОХ, ОY, ОZ вдоль ребер ОА, ОВ, ОС соответственно. Пусть вектор падающего луча света равен \(\vec{a}_1 = \{x, y, z\}\). При отражении от грани АОВ (плоскость XY) изменяется только z-компонента вектора на противоположную, так что отраженный вектор равен \(\vec{a}_2 = \{x, y, -z\}\). При отражении от грани АОС (плоскость XZ) изменяется только y-компонента, и вектор становится \(\vec{a}_3 = \{x, -y, -z\}\). При отражении от грани ВОС (плоскость YZ) изменяется только x-компонента, и вектор становится \(\vec{a}_4 = \{-x, -y, -z\}\). Вектор \(\vec{a}_4\) равен \(- \{x, y, z\}\), то есть \(\vec{a}_4 = -\vec{a}_1\). Таким образом, луч света выходит из тетраэдра в направлении, противоположном направлению входящего луча. Порядок отражений от граней не влияет на конечный результат.
Рассмотрим тетраэдр ОАВС, у которого все плоские углы при вершине О прямые. Грани ОАВ, ОАС, ОВС являются зеркальными, а основание АВС прозрачное. Необходимо доказать, что луч света, вошедший через основание АВС, после отражения от всех трех зеркальных граней выйдет из тетраэдра в направлении, противоположном направлению входящего луча.
Для решения задачи введем прямоугольную декартову систему координат с началом в точке О. Направим ось ОХ вдоль ребра ОА, ось ОY вдоль ребра ОВ и ось ОZ вдоль ребра ОС. Таким образом, грани ОАВ, ОАС, ОВС совпадают с координатными плоскостями XY, XZ, YZ соответственно.
Пусть вектор падающего луча света, входящего в тетраэдр, имеет координаты \(\vec{a}_1 = \{x, y, z\}\). Этот вектор направлен внутрь тетраэдра.
Первое отражение происходит от одной из зеркальных граней. Предположим, что первым отражением является отражение от грани ОАВ, которая лежит в плоскости XY. При отражении от плоскости XY у вектора меняется на противоположную только z-компонента, а x и y компоненты остаются без изменения. Следовательно, вектор луча после отражения от грани ОАВ, обозначим его \(\vec{a}_2\), будет иметь координаты \(\vec{a}_2 = \{x, y, -z\}\).
Далее луч \(\vec{a}_2\) отражается от другой зеркальной грани. Пусть это будет грань ОАС, которая лежит в плоскости XZ. При отражении от плоскости XZ у вектора меняется на противоположную только y-компонента, а x и z компоненты остаются без изменения. Вектор луча после отражения от грани ОАС, обозначим его \(\vec{a}_3\), будет иметь координаты \(\vec{a}_3 = \{x, -y, -z\}\).
Наконец, луч \(\vec{a}_3\) отражается от оставшейся зеркальной грани ОВС, которая лежит в плоскости YZ. При отражении от плоскости YZ у вектора меняется на противоположную только x-компонента, а y и z компоненты остаются без изменения. Вектор луча после отражения от грани ОВС, обозначим его \(\vec{a}_4\), будет иметь координаты \(\vec{a}_4 = \{-x, -y, -z\}\).
Сравним конечный вектор \(\vec{a}_4\) с исходным вектором \(\vec{a}_1\). Мы видим, что \(\vec{a}_4 = \{-x, -y, -z\}\). Вынеся за скобки множитель \(-1\), получим \(\vec{a}_4 = -\{x, y, z\}\). Поскольку \(\{x, y, z\}\) является вектором \(\vec{a}_1\), мы имеем \(\vec{a}_4 = -\vec{a}_1\).
Это означает, что вектор выходящего луча \(\vec{a}_4\) направлен в точности в противоположную сторону относительно вектора входящего луча \(\vec{a}_1\).
Важно отметить, что порядок, в котором происходят отражения от трех зеркальных граней, не влияет на конечный результат. Например, если бы луч сначала отразился от грани ОАС (XZ), затем от ОВС (YZ), и только потом от ОАВ (XY), последовательные векторы были бы:
Исходный: \(\vec{a}_1 = \{x, y, z\}\)
Отражение от ОАС (XZ): \(\{x, -y, z\}\)
Отражение от ОВС (YZ): \(\{-x, -y, z\}\)
Отражение от ОАВ (XY): \(\{-x, -y, -z\}\)
Конечный вектор снова равен \(\{-x, -y, -z\}\), что равно \(- \vec{a}_1\). Любой другой порядок отражений также приведет к тому же результату.
Таким образом, после отражения от всех трех зеркальных граней тетраэдра, луч света выходит из тетраэдра по направлению, противоположному направлению входящего луча, что и требовалось доказать.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.