ГДЗ по Геометрии 11 класс Номер 789 Атанасян — Подробные Ответы

Используя векторы, докажите, что сумма квадратов четырёх диагоналей параллелепипеда равна сумме квадратов двенадцати его рёбер.

Дано:
\(ABCDA_1B_1C_1D_1\) — параллелепипед;

Доказать:
\(S_{\text{кв.ди.}} = S_{\text{кв.реб}};\)

Доказательство:
1) \(\vec{AB} = \vec{a}, \vec{AD} = \vec{b}\) и \(\vec{AA_1} = \vec{c}:\)
\(\vec{AC_1} = \vec{AB} + \vec{BC} + \vec{CC_1} = \vec{a} + \vec{b} + \vec{c};\)
\(\vec{BD_1} = \vec{BA} + \vec{AD} + \vec{DD_1} = -\vec{a} + \vec{b} + \vec{c};\)
\(\vec{CA_1} = \vec{CD} + \vec{DA} + \vec{AA_1} = -\vec{a} — \vec{b} + \vec{c};\)
\(\vec{DB_1} = \vec{DC} + \vec{CB} + \vec{BB_1} = \vec{a} — \vec{b} + \vec{c};\)
2) Найдем квадраты этих векторов:
\({\vec{AC_1}}^2 = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 + 2\vec{a}\vec{b} + 2\vec{a}\vec{c} + 2\vec{c}\vec{b};\)
\({\vec{BD_1}}^2 = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 — 2\vec{a}\vec{b} — 2\vec{a}\vec{c} + 2\vec{c}\vec{b};\)
\({\vec{CA_1}}^2 = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 + 2\vec{a}\vec{b} — 2\vec{a}\vec{c} — 2\vec{c}\vec{b};\)
\({\vec{DB_1}}^2 = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 — 2\vec{a}\vec{b} + 2\vec{a}\vec{c} — 2\vec{c}\vec{b};\)
3) Сумма квадратов диагоналей:
\(S_{\text{кв.диагоналей}} = 4\vec{a}^2 + 4\vec{b}^2 + 4\vec{c}^2;\)
Что и требовалось доказать.

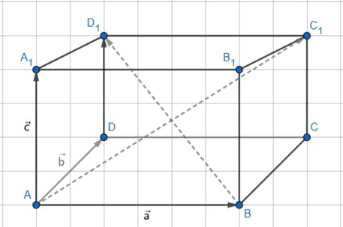
Рассмотрим параллелепипед \(ABCDA_1B_1C_1D_1\). Введем векторы, совпадающие с ребрами, выходящими из одной вершины, например, из вершины A. Пусть \(\vec{AB} = \vec{a}\), \(\vec{AD} = \vec{b}\) и \(\vec{AA_1} = \vec{c}\). Длины этих ребер равны \(|\vec{a}|\), \(|\vec{b}|\) и \(|\vec{c}|\) соответственно. В параллелепипеде 12 ребер: четыре ребра имеют длину \(|\vec{a}|\), четыре — \(|\vec{b}|\) и четыре — \(|\vec{c}|\). Сумма квадратов длин всех ребер равна \(4|\vec{a}|^2 + 4|\vec{b}|^2 + 4|\vec{c}|^2\). Поскольку квадрат длины вектора равен скалярному квадрату этого вектора, то есть \(|\vec{a}|^2 = \vec{a}^2\), \(|\vec{b}|^2 = \vec{b}^2\) и \(|\vec{c}|^2 = \vec{c}^2\), сумма квадратов длин ребер равна \(4\vec{a}^2 + 4\vec{b}^2 + 4\vec{c}^2\).

Теперь рассмотрим диагонали параллелепипеда. В параллелепипеде четыре диагонали, соединяющие противоположные вершины: \(AC_1\), \(BD_1\), \(CA_1\), \(DB_1\). Выразим векторы этих диагоналей через введенные базисные векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\).

Вектор диагонали \(AC_1\) можно представить как сумму векторов \(\vec{AB} + \vec{BC} + \vec{CC_1}\). Поскольку \(\vec{BC}\) параллелен и равен по длине \(\vec{AD}\), то \(\vec{BC} = \vec{b}\). Аналогично, \(\vec{CC_1}\) параллелен и равен по длине \(\vec{AA_1}\), то \(\vec{CC_1} = \vec{c}\). Следовательно, \(\vec{AC_1} = \vec{a} + \vec{b} + \vec{c}\).

Вектор диагонали \(BD_1\) можно представить как сумму векторов \(\vec{BA} + \vec{AD} + \vec{DD_1}\). Вектор \(\vec{BA}\) противоположен вектору \(\vec{AB}\), поэтому \(\vec{BA} = -\vec{a}\). Вектор \(\vec{AD} = \vec{b}\). Вектор \(\vec{DD_1}\) параллелен и равен по длине \(\vec{AA_1}\), поэтому \(\vec{DD_1} = \vec{c}\). Следовательно, \(\vec{BD_1} = -\vec{a} + \vec{b} + \vec{c}\).

Вектор диагонали \(CA_1\) можно представить как сумму векторов \(\vec{CD} + \vec{DA} + \vec{AA_1}\). Вектор \(\vec{CD}\) параллелен и противоположен вектору \(\vec{AB}\), поэтому \(\vec{CD} = -\vec{a}\). Вектор \(\vec{DA}\) противоположен вектору \(\vec{AD}\), поэтому \(\vec{DA} = -\vec{b}\). Вектор \(\vec{AA_1} = \vec{c}\). Следовательно, \(\vec{CA_1} = -\vec{a} — \vec{b} + \vec{c}\).

Вектор диагонали \(DB_1\) можно представить как сумму векторов \(\vec{DC} + \vec{CB} + \vec{BB_1}\). Вектор \(\vec{DC}\) параллелен и равен по длине вектору \(\vec{AB}\), поэтому \(\vec{DC} = \vec{a}\). Вектор \(\vec{CB}\) параллелен и противоположен вектору \(\vec{AD}\), поэтому \(\vec{CB} = -\vec{b}\). Вектор \(\vec{BB_1}\) параллелен и равен по длине вектору \(\vec{AA_1}\), поэтому \(\vec{BB_1} = \vec{c}\). Следовательно, \(\vec{DB_1} = \vec{a} — \vec{b} + \vec{c}\).

Теперь найдем квадраты длин этих диагоналей, что равно скалярному квадрату соответствующих векторов.
Квадрат длины диагонали \(AC_1\): \(|\vec{AC_1}|^2 = (\vec{a} + \vec{b} + \vec{c})^2 = (\vec{a} + \vec{b} + \vec{c}) \cdot (\vec{a} + \vec{b} + \vec{c}) = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 +\)
\(+ 2\vec{a}\vec{b} + 2\vec{a}\vec{c} + 2\vec{b}\vec{c}\).
Квадрат длины диагонали \(BD_1\): \(|\vec{BD_1}|^2 = (-\vec{a} + \vec{b} + \vec{c})^2 = (-\vec{a} + \vec{b} +\)
\(+ \vec{c}) \cdot (-\vec{a} + \vec{b} + \vec{c}) = (-\vec{a})^2 + \vec{b}^2 + \vec{c}^2 + 2(-\vec{a})\vec{b} + 2(-\vec{a})\vec{c} + 2\vec{b}\vec{c} =\)
\(= \vec{a}^2 + \vec{b}^2 + \vec{c}^2 — 2\vec{a}\vec{b} — 2\vec{a}\vec{c} + 2\vec{b}\vec{c}\).
Квадрат длины диагонали \(CA_1\): \(|\vec{CA_1}|^2 = (-\vec{a} — \vec{b} + \vec{c})^2 = (-\vec{a} — \vec{b} + \vec{c}) \cdot (-\vec{a} — \vec{b} + \vec{c}) = (-\vec{a})^2 + (-\vec{b})^2 +\)
\(+ \vec{c}^2 + 2(-\vec{a})(-\vec{b}) + 2(-\vec{a})\vec{c} + 2(-\vec{b})\vec{c} = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 + 2\vec{a}\vec{b} — 2\vec{a}\vec{c} — 2\vec{b}\vec{c}\).
Квадрат длины диагонали \(DB_1\): \(|\vec{DB_1}|^2 = (\vec{a} — \vec{b} + \vec{c})^2 = (\vec{a} — \vec{b} + \vec{c}) \cdot (\vec{a} — \vec{b} + \vec{c}) = \vec{a}^2 + (-\vec{b})^2 + \)
\(+\vec{c}^2 + 2\vec{a}(-\vec{b}) + 2\vec{a}\vec{c} + 2(-\vec{b})\vec{c} = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 — 2\vec{a}\vec{b} + 2\vec{a}\vec{c} — 2\vec{b}\vec{c}\).

Теперь сложим квадраты длин всех четырех диагоналей:
\(|\vec{AC_1}|^2 + |\vec{BD_1}|^2 + |\vec{CA_1}|^2 + |\vec{DB_1}|^2 = (\vec{a}^2 + \vec{b}^2 + \vec{c}^2 + 2\vec{a}\vec{b} + 2\vec{a}\vec{c} + 2\vec{b}\vec{c})+\)
\( + (\vec{a}^2 + \vec{b}^2 + \vec{c}^2 — 2\vec{a}\vec{b} — 2\vec{a}\vec{c} + 2\vec{b}\vec{c}) + (\vec{a}^2 + \vec{b}^2 + \vec{c}^2 + \)
\(+2\vec{a}\vec{b} — 2\vec{a}\vec{c} — 2\vec{b}\vec{c}) + (\vec{a}^2 + \vec{b}^2 + \vec{c}^2 — 2\vec{a}\vec{b} + 2\vec{a}\vec{c} — 2\vec{b}\vec{c})\).
При сложении этих выражений видно, что все члены, содержащие скалярные произведения (\(2\vec{a}\vec{b}\), \(2\vec{a}\vec{c}\), \(2\vec{b}\vec{c}\)), взаимно уничтожаются:
\(2\vec{a}\vec{b} — 2\vec{a}\vec{b} + 2\vec{a}\vec{b} — 2\vec{a}\vec{b} = 0\)
\(2\vec{a}\vec{c} — 2\vec{a}\vec{c} — 2\vec{a}\vec{c} + 2\vec{a}\vec{c} = 0\)
\(2\vec{b}\vec{c} + 2\vec{b}\vec{c} — 2\vec{b}\vec{c} — 2\vec{b}\vec{c} = 0\)
Остаются только члены с квадратами векторов:
\(|\vec{AC_1}|^2 + |\vec{BD_1}|^2 + |\vec{CA_1}|^2 + |\vec{DB_1}|^2 = \vec{a}^2 + \vec{b}^2 + \vec{c}^2 + \vec{a}^2 + \vec{b}^2 + \vec{c}^2 + \vec{a}^2+\)
\( + \vec{b}^2 + \vec{c}^2 + \vec{a}^2 + \vec{b}^2 + \vec{c}^2 = 4\vec{a}^2 + 4\vec{b}^2 + 4\vec{c}^2\).

Таким образом, сумма квадратов длин диагоналей параллелепипеда равна \(4\vec{a}^2 + 4\vec{b}^2 + 4\vec{c}^2\). Ранее мы установили, что сумма квадратов длин всех ребер параллелепипеда также равна \(4\vec{a}^2 + 4\vec{b}^2 + 4\vec{c}^2\).
Следовательно, сумма квадратов длин диагоналей параллелепипеда равна сумме квадратов длин всех его ребер. Что и требовалось доказать.