
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 785 Атанасян — Подробные Ответы
Докажите, что центры граней правильного додекаэдра являются вершинами правильного икосаэдра.
1) Прямая, соединяющая две противоположные вершины правильного додекаэдра, является осью симметрии третьего порядка, то есть додекаэдр совмещается с собой при повороте на \(120°\).
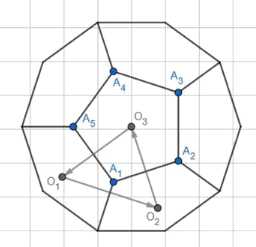
2) Пусть додекаэдр вращается вокруг оси, проходящей через вершину \(A_1\), тогда при повороте на \(120°\) точка \(O_1\) переходит в точку \(O_2\), \(O_2\) в \(O_3\) и \(O_3\) в \(O_1\), следовательно треугольник \(O_1O_2O_3\) является равносторонним.
3) Аналогично для осей, проходящих через каждую вершину, значит каждые точки центров трех соседних граней додекаэдра образуют правильный треугольник.
4) Двенадцать точек центров граней образуют двадцать правильных треугольников, они являются вершинами правильного икосаэдра, что и требовалось доказать.
Дано: правильный додекаэдр \(A_1A_2…A_{20}\) и центры граней \(O_1, O_2, …, O_{12}\). Требуется доказать, что точки \(O_1O_2…O_{12}\) образуют правильный икосаэдр.
Доказательство:
1) Прямая, соединяющая две противоположные вершины правильного додекаэдра, является осью симметрии третьего порядка, то есть додекаэдр совмещается с собой при повороте на \(120°\). Это означает, что если додекаэдр вращается вокруг оси, проходящей через вершину \(A_1\), то при повороте на \(120°\) точка \(O_1\) переходит в точку \(O_2\), \(O_2\) в \(O_3\) и \(O_3\) в \(O_1\).
2) Поскольку при повороте на \(120°\) точки \(O_1\), \(O_2\) и \(O_3\) переходят друг в друга, то треугольник \(O_1O_2O_3\) является равносторонним.
3) Аналогично, для каждой вершины додекаэдра \(A_i\) центры трех граней, сходящихся в этой вершине, образуют равносторонний треугольник \(O_jO_kO_l\).
4) Таким образом, двенадцать точек центров граней додекаэдра \(O_1, O_2, …, O_{12}\) образуют двадцать равносторонних треугольников. Эти треугольники являются вершинами правильного икосаэдра. Следовательно, точки \(O_1O_2…O_{12}\) образуют правильный икосаэдр, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!