
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 783 Атанасян — Подробные Ответы
Внутри куба с ребром 1 см расположена ломаная, причём любая плоскость, параллельная любой грани куба, пересекает её не более чем в одной точке. Докажите, что длина ломаной меньше 3 см. Докажите, что можно построить ломаную, обладающую указанным свойством, длина которой сколь угодно мало отличается от 3 см.
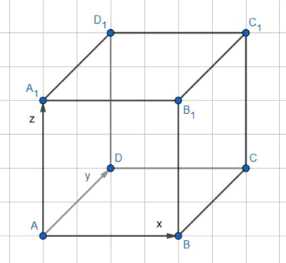
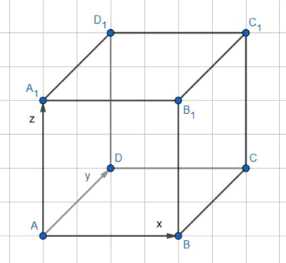
1) Направим оси координат из вершины куба А: ОХ — вдоль AB, OY — вдоль AD, OZ — вдоль AA1.
2) Пусть x, y, z — проекции ломаной на оси координат.
3) По условию каждая плоскость, параллельная любой грани куба, пересекает ломаную не более, чем в одной точке, значит у проекций отрезков нет общих точек.
4) По неравенству треугольника, каждый отрезок ломаной будет меньше суммы длин его проекций: \(x + y + z < 3\), \(l < 3\) см.
5) Если вести ломаную достаточно близко к граням куба, тогда длина каждого отрезка будет стремиться к 1 см, а их сумма к 3 см, что и требовалось доказать.
Полное пошаговое решение:
Дано: Куб ABCDA1B1C1D1, где сторона куба a = 1 см. Требуется доказать, что длина ломаной меньше 3 см.
Шаг 1: Направим оси координат из вершины куба А. Пусть ось ОХ направлена вдоль ребра AB, ось OY — вдоль ребра AD, а ось OZ — вдоль ребра AA1.
Шаг 2: Рассмотрим проекции ломаной на оси координат. Пусть x, y, z — проекции ломаной на оси ОХ, OY и OZ соответственно.
Шаг 3: По условию, каждая плоскость, параллельная любой грани куба, пересекает ломаную не более, чем в одной точке. Это означает, что проекции отрезков ломаной не имеют общих точек.
Шаг 4: Применим неравенство треугольника к каждому отрезку ломаной. Согласно этому неравенству, длина любого отрезка ломаной меньше суммы длин его проекций на оси координат:
\(x + y + z < 3\) Шаг 5: Поскольку длина каждого ребра куба равна 1 см, то длина любого отрезка ломаной, проведенной внутри куба, не превышает 1 см. Следовательно, сумма длин всех отрезков ломаной, то есть длина ломаной, будет меньше 3 см:
\(l < 3\) см Таким образом, мы доказали, что длина ломаной меньше 3 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!