ГДЗ по Геометрии 11 класс Номер 782 Атанасян — Подробные Ответы

Докажите, что из конечного числа попарно различных кубов нельзя составить прямоугольный параллелепипед.

Доказать, что из конечного числа попарно различных кубов нельзя составить прямоугольный параллелепипед, можно следующим образом:
1) Пусть ABCD — грань параллелепипеда, составленного из кубов.
2) Пусть к грани ABCD примыкает наименьший куб с ребром длины \(a\).
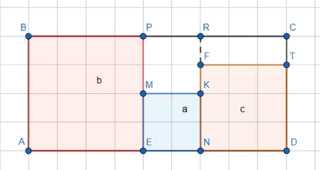
3) К этому кубу с ребром \(a\) можно приставить два других куба с ребрами \(b\) и \(c\), которые будут прилегать к граням BPEA и FTDN соответственно.
4) Чтобы заполнить промежутки PRKM и RCTF, потребуются кубы со стороной, равной или меньшей, чем \(a\). Но это невозможно, так как получается противоречие.
Следовательно, составить параллелепипед из конечного числа таких кубов невозможно.

Доказательство того, что из конечного числа попарно различных кубов нельзя составить прямоугольный параллелепипед, можно провести следующим образом:

Предположим, что существует прямоугольный параллелепипед, составленный из конечного числа попарно различных кубов. Рассмотрим одну из граней этого параллелепипеда, назовем ее ABCD.

К грани ABCD примыкает один из кубов, назовем его наименьшим кубом. Пусть длина ребра этого куба равна \(a\).

Теперь к этому наименьшему кубу с ребром длины \(a\) можно приставить два других куба с ребрами длины \(b\) и \(c\), которые будут прилегать к граням BPEA и FTDN соответственно.

Чтобы заполнить промежутки PRKM и RCTF, потребуются кубы со стороной, равной или меньшей, чем \(a\). Но это невозможно, так как получается противоречие: для заполнения этих промежутков нужны кубы, размер которых меньше, чем размер наименьшего куба, входящего в параллелепипед.

Следовательно, составить прямоугольный параллелепипед из конечного числа попарно различных кубов невозможно, что и требовалось доказать.