
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 781 Атанасян — Подробные Ответы
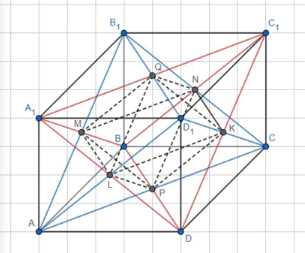
Дан куб ABCDA1B1C1D1. Докажите, что пересечение тетраэдров AB1CD1 и C1BALD есть правильный октаэдр.
1) Тетраэдры пересекаются в точках M, N, K, P, L и Q.
2) Отрезки A1C1 и B1D1 являются диагоналями грани куба, значит точка Q — пересечение диагоналей грани A1B1D1C1, отсюда A1Q = QC1 и B1Q = QD1, аналогично для остальных точек пересечения, следовательно все точки октаэдра лежат на серединах граней куба.
3) Расстояние между серединами соседних граней куба равняется: \(ML = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{a}{2}\right)^2} = \frac{a}{\sqrt{2}}\).
4) Аналогично для всех остальных граней, то есть тело MNKPLQ имеет 8 вершин и расстояние между соседними вершинами равно \(\frac{a}{\sqrt{2}}\), значит данное тело является октаэдром.
Дано: куб ABCDA1B1C1D1; тетраэдры AB1CD1 и C1BA1D.
Доказать: AB1CD1 ∩ C1BA1D — правильный октаэдр.
Доказательство:
1) Рассмотрим тетраэдры, образованные пересечением граней куба. Эти тетраэдры пересекаются в точках M, N, K, P, L и Q.
2) Отрезки A1C1 и B1D1 являются диагоналями грани куба ABCD. Значит, точка Q является пересечением диагоналей грани A1B1D1C1. Отсюда следует, что A1Q = QC1 и B1Q = QD1. Аналогично для остальных точек пересечения, следовательно, все точки октаэдра лежат на середине граней куба.
3) Пусть сторона квадрата равна a. Тогда расстояние между серединами соседних граней куба равняется:
\(ML = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{a}{2}\right)^2} = \frac{a}{\sqrt{2}}\)
4) Аналогично для всех остальных граней, то есть тело MNKPLQ имеет 8 вершин и расстояние между соседними вершинами равно \(\frac{a}{\sqrt{2}}\). Это означает, что данное тело является правильным октаэдром.
Таким образом, доказано, что пересечение тетраэдров AB1CD1 и C1BA1D является правильным октаэдром.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!