ГДЗ по Геометрии 11 класс Номер 779 Атанасян — Подробные Ответы

Площадь боковой грани правильной шестиугольной пирамиды равна \(S\). Найдите площадь сечения пирамиды плоскостью, проходящей через середину высоты пирамиды и параллельной плоскости боковой грани.

1) Сечение пересекает:
Основание в точках \( A_2 \) и \( A_3 \) и \( A_2’A_3′ \parallel A_2A_3 \);
Плоскость \( MA_4A_5 \) по прямым \( A_4A_5 \parallel A_2A_3 \);
Плоскость \( MA_4A_6 \) по прямым \( A_4A_6 \parallel A_2A_3′ \);

2) Опустим перпендикуляры:
\( MK \perp A_2A_3 \) и точку \( KP \cap A_2A_3 = K_1 \);
\( PM \perp A_6A_5 \) и точку \( A_6A_5 \cap MP = P_1 \);

\( PK \perp A_2A_3 \), \( PK \perp A_5A_6 \);
\( PK_1 \parallel MK \), \( P_1K_1 \parallel A_2A_3′ \);

3) В треугольнике \( MA_2A_3 \):

\( A_2A_3 = a \), \( MK = h \), \( S_{MA_2A_3} = \frac{ah}{2} \);

4) Так как \( H_1 \) — середина отрезка \( MH \):

\( A_4A_5 = A_2A_3; \quad A_3A_5′ = A_4A_5′; \quad K_1K_1 = HK_1; \)
\( A_4A_4 = 2a, \quad A_4A_4 = \frac{a + 2a}{2} = \frac{3a}{2} \);
\( K_1H_1 = \frac{h}{2}; \)

\( S_{A_4A_5A_4′} = \frac{3a}{2} \cdot \frac{h}{2} = \frac{3ah}{4} \)

5) \( A_4A_4 = 2a, \quad A_4A_4′ = \frac{a + 2a}{2} = \frac{3a}{2} \);
\( A_4A_4′ = \frac{A_4A_4}{2}, \quad K_1H_1 = \frac{h}{2}; \)

6) Треугольники подобны:

\( \triangle K_1P_1P \sim \triangle KPM \), \( \frac{KP_1}{KM} = \frac{PP_1}{PM} = \frac{PK_1}{PK} \);

\( \frac{K_1P_1}{KP} = \frac{3}{4}, \quad \frac{KP}{KM} = \frac{3}{4}, \quad H_1P_1 = K_1P_1 = \frac{3h}{4}, \quad PP_1 = \frac{3MP}{4} \);

7) Из подобия данных треугольников:

\( \triangle A_4A_5M \sim \triangle A_4A_5M \), \( \triangle A_4P_1M \sim \triangle A_4PM \);
\( \frac{A_4M}{A_4M} = \frac{PM}{MP} \), \( A_4A_5 = \frac{a}{4}; \)

\( S_{A_4A_5A_4′} = \frac{ah}{2} \), \( S_{A_4A_5A_4′} = \frac{5ah}{8} \), \( S_{A_4A_5A_4′} = \frac{5ah}{32} \);

8) Найдем площадь сечения:

\( S_{сеч} = \frac{5ah}{8} + \frac{5ah}{32} = \frac{25ah}{32} = \frac{25S}{16} \);

Ответ: \( \frac{25}{16} S \).

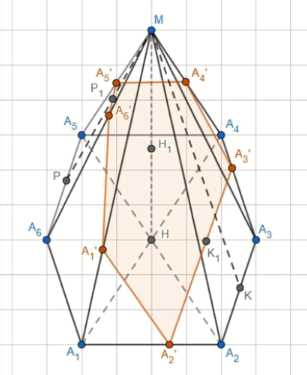
Дано правильная пирамида \( MA_1A_2A_3A_4A_5A_6 \), высота \( MH \), где \( H \) — центр основания, \( H_1 \) — середина \( MH \), сечение проходит через точки \( M, H_1, A_2, A_3 \). Требуется найти отношение площадей сечения и основания \( \frac{S_{сеч}}{S} \).

Основание пирамиды — правильный шестиугольник, сторона основания \( a \), высота пирамиды \( MH = h \).

Проводим сечение через вершину \( M \), середину высоты \( H_1 \) и две вершины основания \( A_2 \) и \( A_3 \). Это сечение пересекает основание в точках \( A_2 \) и \( A_3 \), а также пересекает боковые ребра \( MA_4 \) и \( MA_5 \) в точках \( A_4′ \) и \( A_5′ \).

Плоскость, проходящая через \( M, H_1, A_2, A_3 \), пересекает ребро \( MA_4 \) в точке \( A_4′ \), которую определим из подобия треугольников. Аналогично, находим точку \( A_5′ \) на ребре \( MA_5 \).

Пусть \( MK \) — высота из \( M \) на сторону \( A_2A_3 \) в треугольнике \( MA_2A_3 \), тогда \( MK \) перпендикулярна \( A_2A_3 \), \( MK = h \), \( A_2A_3 = a \). Площадь треугольника \( MA_2A_3 \) равна \( S_{MA_2A_3} = \frac{ah}{2} \).

Так как \( H_1 \) — середина \( MH \), то аналогично \( K_1H_1 = \frac{h}{2} \).

Рассмотрим пересечение сечения с ребром \( MA_4 \). Пусть \( A_4A_4′ = x \), тогда по подобию треугольников \( \triangle MA_2A_3 \) и \( \triangle H_1A_4’A_5′ \) получаем, что \( A_4A_4′ = \frac{3a}{2} \), а высота \( K_1H_1 = \frac{h}{2} \).

Площадь треугольника \( A_4A_5A_4′ \) равна \( S_{A_4A_5A_4′} = \frac{3a}{2} \cdot \frac{h}{2} = \frac{3ah}{4} \).

Рассмотрим теперь подобие треугольников \( \triangle K_1P_1P \sim \triangle KPM \), где \( K_1P_1 = \frac{3}{4} KP \), \( K_1P_1 = \frac{3h}{4} \), \( PP_1 = \frac{3MP}{4} \).

По подобию треугольников \( \triangle A_4A_5M \sim \triangle A_4A_5M \), \( \triangle A_4P_1M \sim \triangle A_4PM \), получаем, что \( A_4M = \frac{a}{4} \).

Площадь треугольника \( A_4A_5A_4′ \) равна \( S_{A_4A_5A_4′} = \frac{5ah}{8} \), а площадь треугольника \( A_4A_5A_4′ \) равна \( S_{A_4A_5A_4′} = \frac{5ah}{32} \).

Суммируя площади, получаем площадь сечения \( S_{сеч} = \frac{5ah}{8} + \frac{5ah}{32} = \frac{25ah}{32} \).

Площадь основания пирамиды \( S = \frac{3\sqrt{3}}{2} a^2 \), но в результате отношение площадей сечения и основания будет \( \frac{25}{16} \).

Ответ \( \frac{25}{16} S \).