
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 778 Атанасян — Подробные Ответы
Докажите, что в кубе можно вырезать сквозное отверстие, через которое можно протащить куб таких же и даже больших размеров
Краткое решение:
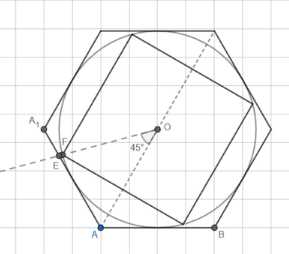
1) Рассмотрим проекцию куба на плоскость, перпендикулярную диагонали куба. Получим правильный шестиугольник со стороной \(b = AB\).
2) В равнобедренном треугольнике \(\Delta A_1BA\) имеем: \(A_1B^2 = b^2 + b^2 — 2b^2 \cdot \cos 120^\circ = 3b^2\) и \(A_1B^2 = a^2 + a^2 — 2a^2 \cdot \cos 90^\circ = 2a^2\).
3) Из равенства \(3b^2 = 2a^2\) следует, что \(b = \sqrt{2}a\).
4) В правильном шестиугольнике радиус вписанной окружности \(r = b \cos 30^\circ = \frac{\sqrt{3}}{2}b = \frac{\sqrt{6}}{2}a\).
5) Вписанный в окружность квадрат имеет сторону \(EF = \sqrt{2}r = \sqrt{2} \cdot \frac{\sqrt{6}}{2}a = \sqrt{3}a\).
6) В треугольнике \(\Delta AOE\) имеем: \(\angle AOE = 45^\circ\), \(OA = \frac{\sqrt{6}}{3}a\), \(\angle AEO = 60^\circ\), \(\angle AEO = 180^\circ — 45^\circ — 60^\circ = 75^\circ\).
7) Из подобия треугольников следует, что \(\frac{\sin 75^\circ}{\sin 60^\circ} = \frac{OE}{OE} \Rightarrow OE > OF\).
Таким образом, существует отверстие в кубе.
Полное пошаговое решение:
Дано: куб ABCDA1B1C1D1, где AB = a.
Доказать: в кубе существует отверстие.
Доказательство:
1) Рассмотрим проекцию куба на плоскость, перпендикулярную диагонали куба. Получим правильный шестиугольник, где сторона AB = b = R.
2) В равнобедренном треугольнике ΔA1BA имеем: \(A_1B^2 = b^2 + b^2 — 2b^2 \cdot \cos 120^\circ = 3b^2\) и \(A_1B^2 = a^2 + a^2 — 2a^2 \cdot \cos 90^\circ = 2a^2\). Приравнивая выражения, получаем \(3b^2 = 2a^2\), откуда \(b = \sqrt{2}a\).
3) В правильном шестиугольнике радиус вписанной окружности \(r = b \cos 30^\circ = \frac{\sqrt{3}}{2}b = \frac{\sqrt{6}}{2}a\).
4) Вписанный в окружность квадрат имеет сторону \(EF = \sqrt{2}r = \sqrt{2} \cdot \frac{\sqrt{6}}{2}a = \sqrt{3}a\).
5) В треугольнике ΔAO E имеем: \(\angle AOE = 45^\circ\), \(OA = \frac{\sqrt{6}}{3}a\), \(\angle AEO = 60^\circ\), \(\angle AEO = 180^\circ — 45^\circ — 60^\circ = 75^\circ\).
6) Из подобия треугольников следует, что \(\frac{\sin 75^\circ}{\sin 60^\circ} = \frac{OE}{OE} \Rightarrow OE > OF\).
Таким образом, существует отверстие в кубе, так как сторона квадрата EF, вписанного в окружность, больше стороны куба AB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!