ГДЗ по Геометрии 11 класс Номер 777 Атанасян — Подробные Ответы

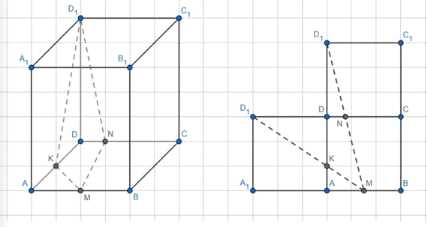
Комната имеет форму куба. Паук, сидящий в середине ребра, хочет, двигаясь по кратчайшему пути, поймать муху, сидящую в одной из самых удалённых от паука вершин куба. Как должен двигаться паук?

Решение:
1) Обозначим сторону куба как \(a\).
2) Точки \(N\) и \(K\) являются пересечениями прямых \(MD_1\) и \(AD\), \(MD_1\) и \(CD\) соответственно.
3) В прямоугольном треугольнике \(AMD_1\): \(AD_1 = 2AD = 2a\), \(AM = \frac{1}{2}AB = \frac{a}{2}\), \(D_1M = \sqrt{a^2 + \frac{a^2}{4}} = \frac{\sqrt{17}}{2}a\).
4) В прямоугольном треугольнике \(AD_1A_1M\): \(A_1D_1 = a\), \(A_1M = A_1A + AM = \frac{3}{2}a\).
5) \(A_1A = 2AM\), \(AK \perp D_1A_1\), \(DK = \frac{1}{3}D_1A_1 = \frac{a}{3}\).
6) Кратчайший путь от паука \(M\) к мухе \(D_1\) проходит через точку \(K\), пересекая ближайшее ребро на расстоянии одной трети от ближайшей к пауку вершины, затем по прямой до мухи.

Решение:

1) Дано, что куб ABCDA1B1C1D1, где D1 — муха, M — паук, и M является серединой ребра AB.

2) Обозначим длину ребра куба как \(a\).

3) Для определения положения точек N и K:
— Точка N является пересечением прямых MD1 и AD.
— Точка K является пересечением прямых MD1 и CD.

4) Рассмотрим прямоугольный треугольник AMD1:
— Так как AD1 = 2AD = 2a, то AD1 = 2a.
— Так как AM = 1/2 AB = a/2, то AM = a/2.
— Используя теорему Пифагора, находим длину D1M: \(D_1M = \sqrt{a^2 + \left(\frac{a}{2}\right)^2} = \frac{\sqrt{17}}{2}a\).

5) Рассмотрим прямоугольный треугольник AD1A1M:
— Так как A1D1 = a, то A1D1 = a.
— Так как A1M = A1A + AM = 3a/2, то A1M = 3a/2.

6) Далее находим:
— A1A = 2AM = a.
— AK перпендикулярно D1A1, и DK = 1/3 D1A1 = a/3.

7) Таким образом, кратчайший путь от паука M к мухе D1 проходит через точку K, пересекая ближайшее ребро на расстоянии одной трети от ближайшей к пауку вершины, затем по прямой до мухи.