Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 775 Атанасян — Подробные Ответы
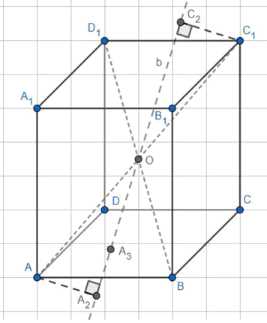
Докажите, что сумма квадратов расстояний от вершин куба до прямой, проходящей через его центр, не зависит от положения этой прямой
Дано: ABCDA,B1C1D1 — куб; b — прямая; \(0 \in b\). Доказать: сумма квадратов расстояний от вершин куба до b — const. Доказательство: 1) \(a\) — сторона куба, \(O\) — центр куба; 2) Построим \(AA_2 \perp b\) и \(CC_2 \perp b\); 3) \(OA\) — половина диагонали куба: \(OD = \frac{\sqrt{3}a}{2}\); 4) \(bn \, ABCD = A_3\); 5) Пусть \(OY — AB\) и \(OX — AD\); 6) \(\triangle A_3OA\): \(A_3A_2 = A_0^2 + A_3^2 — 2 \cos \angle AOA_3 \cdot AO \cdot A_3\), \(A_3^2 = \left(x-\frac{a}{2}\right)^2 + \left(y-\frac{a}{2}\right)^2 + \frac{a^2}{4}\); 7) \(20P \cdot A_3O \cdot \cos \angle A_3OD = -\frac{a^2}{2} — a(x + y)\), \(20P \cdot A_3O \cdot \cos \angle A_3OB = \frac{a^2}{2} + a(x — y)\), \(20P \cdot A_3O \cdot \cos \angle A_3OC = \frac{a^2}{2} + a(x + y)\), \(20P \cdot A_3O \cdot \cos \angle A_3OD = -\frac{a^2}{2} — a(x — y)\), тогда \(4a^2 20P^2 = 40P^2 — A_3^2 \cdot \sum \cos^2 \phi_n\), отсюда \(\sum \sin^2 \phi_n = 4 — \sum \cos^2 \phi_n = 3\); 8) Тогда сумма квадратов расстояний от вершин куба до прямой \(b\) равна \(\frac{32a^2}{3}\).
Дано: ABCDA,B1C1D1 — куб; b — прямая; \(0 \in b\). Доказать: сумма квадратов расстояний от вершин куба до b — const.
Доказательство:
1) Пусть \(a\) — сторона куба, \(O\) — центр куба. Построим \(AA_2 \perp b\) и \(CC_2 \perp b\). Обозначим углы между ребрами куба и прямой \(b\) как \(\phi_1\), \(\phi_2\) и \(\phi_3\).
2) Диагональ куба \(OD = \frac{\sqrt{3}a}{2}\), так как \(OA\) — половина диагонали.
3) Точка \(A_3\) — основание перпендикуляра, опущенного из вершины \(A\) на прямую \(b\).
4) Пусть \(OY — AB\) и \(OX — AD\). Тогда расстояния от вершин куба до прямой \(b\) равны: \(A_3A_2 = x^2 + y^2\), \(A_3B_2 = (a — x)^2 + y^2\), \(A_3C_2 =(a-x)^2 + (a-y)^2\), \(A_3D_2 = x^2 + (a-y)^2\).
5) Рассмотрим \(\triangle A_3OA\): \(A_3A_2 = A_0^2 + A_3^2 — 2 \cos \angle AOA_3 \cdot AO \cdot A_3\), \(A_3^2 = \left(x-\frac{a}{2}\right)^2 + \left(y-\frac{a}{2}\right)^2 + \frac{a^2}{4}\).
6) Найдем выражения для \(20P \cdot A_3O \cdot \cos \angle A_3OD\), \(20P \cdot A_3O \cdot \cos \angle A_3OB\), \(20P \cdot A_3O \cdot \cos \angle A_3OC\) и \(20P \cdot A_3O \cdot \cos \angle A_3OD\).
7) Сложив эти выражения, получим \(4a^2 20P^2 = 40P^2 — A_3^2 \cdot \sum \cos^2 \phi_n\). Отсюда \(\sum \sin^2 \phi_n = 4 — \sum \cos^2 \phi_n = 3\).
8) Таким образом, сумма квадратов расстояний от вершин куба до прямой \(b\) равна \(\frac{32a^2}{3}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.