Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 774 Атанасян — Подробные Ответы
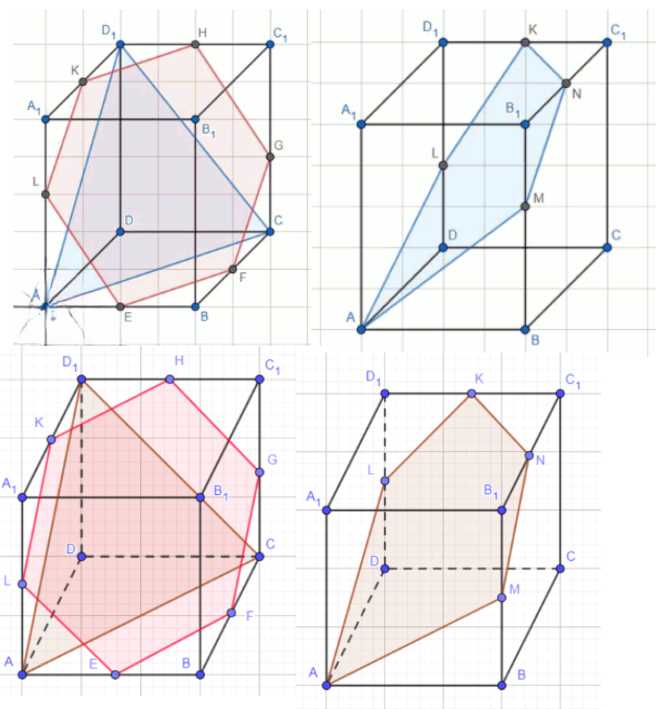
Докажите, что сечением куба может быть правильный треугольник, квадрат, правильный шестиугольник, но не может быть правильный пятиугольник и правильный многоугольник с числом сторон более шести.
1) Сечение ACD1 — правильный треугольник со стороной \(a\sqrt{2}\).
2) Сечения параллельные граням куба — квадраты со стороной \(a\).
3) Сечение LKGHFE — правильный шестиугольник, где \(EF = a/\sqrt{2}\).
4) Сечение AMNKL не может быть правильным многоугольником, так как \(\angle LAM + \angle AMN = 180^\circ\).
5) Куб имеет только 6 граней, значит сечением не может быть правильный многоугольник с большим числом сторон.
Вот подробное решение:
Рассмотрим куб ABCDA1B1C1D1 со стороной \(a\). Для построения всех правильных сечений куба выполним следующие шаги:
1) Сечение ACD1 является правильным треугольником. Сторона треугольника равна \(a\sqrt{2}\), так как диагональ грани куба равна \(a\sqrt{2}\).
2) Сечения, параллельные граням куба, являются квадратами со стороной \(a\). Это объясняется тем, что все ребра куба равны \(a\), и при пересечении плоскостью, параллельной грани, образуются квадраты.
3) Сечение LKGHFE является правильным шестиугольником. Для доказательства этого факта рассмотрим середины ребер куба — точки G, H, K, L, E, F. Так как все эти точки являются серединами ребер, то отрезки, соединяющие их, равны \(a/\sqrt{2}\) по теореме Фалеса. Следовательно, сечение LKGHFE является правильным шестиугольником.
4) Сечение AMNKL не может быть правильным многоугольником. Это объясняется тем, что точки L, K, N, M лежат на ребрах куба, и угол между ними равен \(180^\circ\). Поэтому сумма углов многоугольника не может быть равна \(n(180^\circ — 2\pi/n)\), где \(n\) — число сторон многоугольника.
5) Куб имеет только 6 граней, следовательно, сечением не может быть правильный многоугольник с большим числом сторон.
Таким образом, мы рассмотрели все возможные правильные сечения куба и объяснили, почему они являются правильными или не могут быть правильными многоугольниками.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.