
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 773 Атанасян — Подробные Ответы
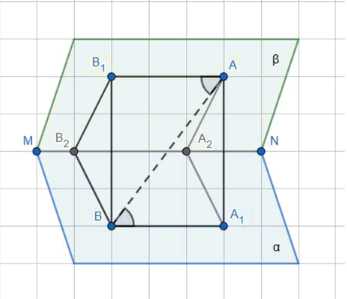
Докажите, что прямая, пересекающая две грани двугранного угла, образует с ними равные углы тогда и только тогда, когда точки пересечения равноудалены от ребра.
1) Построим точку A₁ — проекцию A на α.
2) Построим точку B₁ — проекцию B на β.
3) AA₁ ⊥ α, AA₁ ⊥ MN, BB₁ ⊥ β, BB₁ ⊥ MN.
4) Линейные углы между плоскостями α и β: A₁A₂ ⊥ MN, B₁B₂ ⊥ MN, ∠AA₂A₁ = 2∠BB₂B₁.
5) Из равенства треугольников следует: AA₂ = BB₂/B₁B₂ = A₁A₂, ∆AA₁A₂ = ∆BB₁B₂; AA₁ = BB₁, ∆AA₁B = ∆AB₁B, ∠ABA₁ = ∠BAB₁.
Дано: плоскости α и β, прямая АВ, точки А₁, А₂, В₁, В₂, М и N.
Доказательство:
1) Построим точку А₁ — проекцию точки А на плоскость α. Это позволит нам установить перпендикулярность между прямой АА₁ и плоскостью α.
2) Построим точку В₁ — проекцию точки В на плоскость β. Это позволит нам установить перпендикулярность между прямой ВВ₁ и плоскостью β.
3) Из построения следует, что AA₁ ⊥ α, AA₁ ⊥ MN, BB₁ ⊥ β, BB₁ ⊥ MN.
4) Рассмотрим линейные углы между плоскостями α и β:
— A₁A₂ ⊥ MN
— B₁B₂ ⊥ MN
— ∠AA₂A₁ = 2∠BB₂B₁
5) Из равенства треугольников следует:
— AA₂ = BB₂/B₁B₂ = A₁A₂
— ∆AA₁A₂ = ∆BB₁B₂
— AA₁ = BB₁
— ∆AA₁B = ∆AB₁B
— ∠ABA₁ = ∠BAB₁
Таким образом, мы доказали, что ∠ABA₁ = ∠BAB₁, то есть ∠ABA₁ = ∠BAB₁.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!