
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 772 Атанасян — Подробные Ответы
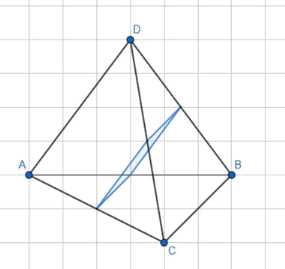
Сколько существует плоскостей, каждая из которых равноудалена от четырёх данных точек, не лежащих в одной плоскости?
Ответ: 7 плоскостей.
Объяснение:
1) Плоскость проходит через середины исходящих из двух вершин ребер, тогда две точки лежат по одну сторону от плоскости, а две других — по другую сторону. Расстояния между параллельными плоскостями, проходящими через данные ребра, равны \(\frac{1}{2}\) высоты тетраэдра. Возможны 3 случая расположения плоскости.
2) По одну сторону от плоскости лежит одна точка, а по другую сторону 3 точки и плоскость проходит через середину ребер, исходящих из одной вершины. Расстояния равны \(\frac{1}{2}\) высоты тетраэдра. Возможны 4 случая расположения плоскости.
Таким образом, общее число возможных плоскостей равно 3 + 4 = 7.
Рассмотрим четыре точки, не лежащие в одной плоскости. Возможны следующие случаи расположения плоскостей:
1) Плоскость проходит через середины ребер, исходящих из двух вершин. В этом случае две точки лежат по одну сторону от плоскости, а две другие — по другую сторону. Расстояния между параллельными плоскостями, проходящими через данные ребра, равны \(\frac{1}{2}\) высоты тетраэдра. Возможны 3 случая расположения плоскости.
2) По одну сторону от плоскости лежит одна точка, а по другую сторону 3 точки. Плоскость проходит через середину ребер, исходящих из одной вершины. Расстояния равны \(\frac{1}{2}\) высоты тетраэдра. Возможны 4 случая расположения плоскости.
Таким образом, общее число возможных плоскостей равно 3 + 4 = 7.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!