
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 771 Атанасян — Подробные Ответы
Через ребро тетраэдра проведена плоскость, разделяющая двугранный угол при этом ребре пополам. Докажите, что она делит противоположное ребро тетраэдра в отношении, равном отношению площадей граней, заключающих этот двугранный угол.
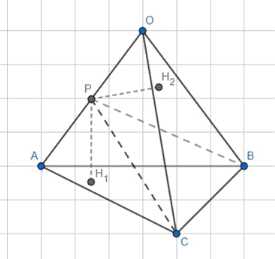
1) Построим прямые PH1 ⊥ ABC и PH2 ⊥ OBC: ∠OBC, PBC = ∠ABC, PBC, PH1 = PH2;
2) Отношение объемов тетраэдров:
\(
\frac{V_{APBC}}{V_{OPBC}} = \frac{1}{3} \cdot \frac{PH1 \cdot S_{ABC}}{PH2 \cdot S_{OBC}} = \frac{S_{ABC}}{S_{OBC}}
\)
3) Высоты h1 и h2 из точек A и O на BPC:
\(
\frac{h1}{h2} = \frac{S_{ABC}}{S_{OBC}} = \frac{AP}{PO’}
\)
Таким образом, \(S_{ABC}/S_{OBC} = AP/PO’\).
Дано: тетраэдр OABC, плоскость СВР делит двугранный угол пополам.
Доказать: \(\frac{S_{ABC}}{S_{OBC}} = \frac{AP}{PO’}\)
Доказательство:
1) Построим прямые PH1 ⊥ ABC и PH2 ⊥ OBC. Тогда ∠OBC, PBC = ∠ABC, PBC, и PH1 = PH2, так как плоскость СВР делит двугранный угол пополам.
2) Рассмотрим отношение объемов тетраэдров APBC и OPBC:
\(
\frac{V_{APBC}}{V_{OPBC}} = \frac{1}{3} \cdot \frac{PH1 \cdot S_{ABC}}{PH2 \cdot S_{OBC}} = \frac{S_{ABC}}{S_{OBC}}
\)
3) Высоты h1 и h2 из точек A и O на ребро BPC:
\(
\frac{h1}{h2} = \frac{S_{ABC}}{S_{OBC}} = \frac{AP}{PO’}
\)
Таким образом, \(\frac{S_{ABC}}{S_{OBC}} = \frac{AP}{PO’}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!