
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 770 Атанасян — Подробные Ответы
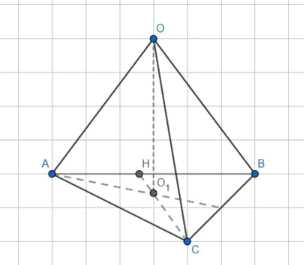
Все плоские углы тетраэдра ОАВС при вершине О равны 90°. Докажите, что площадь треугольника АОВ равна среднему геометрическому площадей треугольников АВС и О1АВ, где О1 — проекция точки О на плоскость АВС.
Дано: ОАВС — тетраэдр; О1 пр. т. О на АВС; ∠AOC = 90°; ∠AOB = 90°. Доказать: \(S^2_{AOB} = S_{ABC} \cdot S_{ABO1}\). Доказательство: 1) О1 — проекция О на АВС: О01 ⊥ АВС; 2) По теореме о трех перпендикулярах: AO ⊥ OB, AO ⊥ OC, OBC ⊥ AO, BC ⊥ AO; BC ⊥ A01 (аналогично докажем BO1 ⊥ AC); 3) По теореме о пересечении высот: BC ⊥ AO1, BO1 ⊥ AC, CO1 ⊥ AB; 4) ∠CHO — угол между плос. АВС и ОАВ; 5) OHO1 ⊥ ABC, OH ⊥ AB, OO1 ⊥ HC; 6) \(S_{AOB} = \frac{1}{2} \cdot AB \cdot OH = \frac{1}{4} \cdot AB^2 \cdot OH^2\), \(S_{ABC} = \frac{1}{2} \cdot AB \cdot CH = \frac{1}{2} \cdot AB \cdot \frac{AB \cdot \cos \angle CHO}{\cos \angle CHO}\), \(S_{ABO1} = \frac{1}{2} \cdot AB \cdot O1H = \frac{AB}{2} \cdot OH \cos \angle CHO\), \(S^2_{AOB} = \frac{1}{4} \cdot AB^2 \cdot OH^2 = S^2_{AOB}\).
Дано: ОАВС — тетраэдр; О1 — проекция точки О на плоскость АВС; ∠AOC = 90°; ∠AOB = 90°. Требуется доказать: \(S^2_{AOB} = S_{ABC} \cdot S_{ABO1}\).
Доказательство:
1) Так как О1 является проекцией точки О на плоскость АВС, то О01 перпендикулярна плоскости АВС.
2) По теореме о трех перпендикулярах, прямые AO, OB и OC взаимно перпендикулярны, а также прямые BC и AO взаимно перпендикулярны (аналогично можно доказать, что BO1 перпендикулярна AC).
3) Согласно теореме о пересечении высот в тетраэдре, прямые BC, BO1 и CO1 взаимно перпендикулярны.
4) Рассмотрим угол ∠CHO между плоскостями АВС и ОАВ.
5) Так как OHO1 перпендикулярна плоскости АВС, а OH перпендикулярна AB, то OO1 перпендикулярна HC.
6) Вычислим площади треугольников:
\(S_{AOB} = \frac{1}{2} \cdot AB \cdot OH = \frac{1}{4} \cdot AB^2 \cdot OH^2\)
\(S_{ABC} = \frac{1}{2} \cdot AB \cdot CH = \frac{1}{2} \cdot AB \cdot \frac{AB \cdot \cos \angle CHO}{\cos \angle CHO}\)
\(S_{ABO1} = \frac{1}{2} \cdot AB \cdot O1H = \frac{AB}{2} \cdot OH \cos \angle CHO\)
7) Возводя в квадрат первое равенство, получаем: \(S^2_{AOB} = \frac{1}{4} \cdot AB^2 \cdot OH^2 = S_{ABC} \cdot S_{ABO1}\)
Таким образом, доказано, что \(S^2_{AOB} = S_{ABC} \cdot S_{ABO1}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!